Géometrie Analytique

[cececi02]

Bonjour , je n'arrive pas a faire ces exercices et si on pouvait m'aider svp :

I] Dans un repere ortonormal , on donne les points :
A (-1;1) B (3;2) C (-2;5) D (2;6)
Demontrer que ABDC est :
a) Un parallélogramme b) Un carré


II] On donne les points A (-1;2) et B (2;3)
1)Quel est le rayon du Cercle T de centre 1 et passant par B ?
2)Determiner les coordonnées du point C , diamétralement opposé à B sur T .
3)Soit D (-2;5).Montrer que le point D appartient a T .
4)Quelle est la nature du triangle BCD ?

Merci d'avance

[Zebulon]

Bonjour,
pour la I)a, il suffit de montrer que .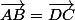
Pour la I)b, il suffit de montrer que le parallélogramme ABCD a un angle droit c'est-à-dire que par exemple (AB) est perpendiculaire à (BC), ce qui se montre avec le produit scalaire, et que deux cêtés consécutifs ont même longueur, ce qui se fait calcul des normes.

Pour la II)1, soit E(1;0). Le rayon du cercle T de centre 1 et passant par B est donc la distance EB.
Pout la II)2, on cherche les coordonnées de C tel que .
Pour la II)3, il suffit de montrer que DE=EB.
Enfin pour la II)4, il faut penser à une propriété qu'on voit au collège:
soit [AB]un segment, alors pour tout point M appartenant au cercle de diamètre [AB], le triangle ABM est rectangle en M.

Bon courage et à bientôt.

[Daragon geoffrey]

slt
pour la une vérifie la relation fondamentale AB=DC (vecteurs) ! aprè avoir calculer les coordonnées de chacun de ces vecteurs, vérifie la relation précédente, si elle est vérifiée : équiv à parallélogramme, puis pour démontrer que ABCD est un carré, vérifie que les 4 côtés ont même longueur (tu calcules pour cela les normes des vecteurs), et enfin que 2 côtés consécutifs forment un angle droit grâce o produit sclaire donné (en repère cartésien orthonormé) par : xx'+yy' (où (x;y) coordonnées du premier vecteur et (x';y')...). il doit être égal à 0 !