Equation différentielle

[Dude]

Bonjour,

Je souhaiterai que l'on m'explique ce qu'est une equation différentielle implicite et ue equation différentielle explicite

je rencontre souvent dans mes cours des démonstrations grace à la forme implicite je ne la comprend pas du tout

merci d'avance

[busard_des_roseaux]

Bj,


il y a un théorème qui dit que si plusieurs quantités réelles
vérifient une équation de la forme
(1)
soient n quantités,
localement, on peut trouver un voisinage dans
du point de la courbe représentative de f où l'équation
se résoud selon une quantité , disons d, qui est , localement
fonction des (n-1) autres variables.

et le théorème des fonctions implicites indique comment calculer
un développement limité (local) de en utilisant les dérivées partielles de

la difficulté, c'est que la fonction n'est définie que dans un petit voisinage du point.

exemple: l'équation d'un cercle donne

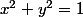
dans le demi-plan supérieur

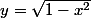
dans le demi-plan droit


dans le demi-plan gauche

etc..

une équation différentielle implicite pourrait être

on voit que la difficulté est de l'écrire sous la forme d'un problème de Cauchy...

[Nightmare]

Salut !

En complément de ce que dit Busard, en terme d'équadiff, on parle d'équation implicite lorsqu'on ne peut pas exprimer la dérivée de plus grand ordre en fonction (continue) des autres.