Equation différentielle

[Nadraffe]

?

[hdci]

Alors :

J'ai trouvé C = -0.04 et quand le calcul est (-0.04)*e^(-0.44*0) + (0.022/0.44)

Quand on calcule avec et , on trouve



On voulait trouver 0,01. Donc c'est que ce n'est pas bon. Au passage, cela devrait être un réflexe que de vérifier que la solution qu'on a trouvé est la bonne solution, en la "testant" dans l'équation (comme ce que je viens de faire).

Par contre, il est vrai que si alors .

Mais à quel moment a-t-on dit que ? La condition initiale, c'est

Au lieu de continuer à manipuler , écrivez donc à quoi est égal , et tant qu'à faire, simplifiez donc l'expression car 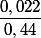ça s'écrit très simplement, avec une fraction d'entiers. Et ça vous donnera une piste au regard de ce que l'énoncé vous demande de trouver.

[Nadraffe]

Merci pour vos réponse et votre aide, mais j'attendrai la correction demain pour pouvoir mieux comprendre, car pour moi l'exercice n'est pas clair du tout.

[TheFanaticV2]

Merci pour vos réponse et votre aide, mais j'attendrai la correction demain pour pouvoir mieux comprendre, car pour moi l'exercice n'est pas clair du tout.

Bonjour ou Bonsoir Nadraffe, j'aimerais savoir si tu as toujours ces exos sur les 10 000 ménages en France. Je sais que ça fait plus d'un an, mais qui ne tente rien n'a rien

[Black Jack]

Oui je suis en spé maths.
Je fais : A²/B = 1/B + 1/B*B donc je peux avoir A² = 1/B + 1/B soit A² = 1/B

Pfff ...

D'abord, A²/B = 1/B + 1/B*B n'est pas équivalent à : A²/B = 1/B + 1/B²

Si on connait les priorités des opérations mathématiques, alors on sait que 1/B*B = 1 (pour tout B différent de 0)
Si on veut écrire 1/B² en se passant du symbole "²", alors il FAUT écrire 1/(B*B)

Ensuite, écrire (en ayant corrigé la faute mentionnée ci-dessus) :
A²/B = 1/B + 1/(B*B) donc je peux avoir A² = 1/B + 1/B
... c'est archi faux.

A²/B = 1/B + 1/(B*B) (avec B différent de 0)
On multiplie les 2 membres par B --->
B*(A²/B) = B*(1/B + 1/(B*B) )
A² = B/B + B/(B*B)
A² = 1 + 1/B
Ou ce qui revient au même : A² = (B+1)/B

Attention que si on veut que A et B soient des nombres réels ... il faut commencer par s'assurer que (B+1)/B >= 0 (ce qui contraint B à être dans ]-oo ; -1] U ]0 ; +oo[)

Et si c'est le cas, on trouve les 2 valeurs possibles de A par ...
*********

Morale :

Vingt fois sur le métier remettez votre ouvrage,
Polissez-le sans cesse, et le repolissez,
Ajoutez quelquefois, et souvent effacez.

Boileau,