Probleme de trigo

[mantus]

hello !

j'ai une petite question par rapport a un probleme de trigo ou je connais tres peu d'informations

je voudrais savoir si il est possible de calculer le rayon et l'angle d'un cercle en connaissant seulement la longueur de l'arc et de la corde de ceux ci

[Ben314]

Bonjour,
La réponse à ta question est.... OUI.
Essaye de le faire et, si tu bute à un moment, vient demander...

P.S. Je vient de réfléchir que la réponse à ta question dépend du sens que tu donne au mot "calculer" :
Tu ne trouvera pas de formule du type "rayon=formule_simple dépendant des longueur de l'arc et de la corde"
Mais tu peut trouver une méthode pour approximer la longueur du rayon conaissant les longueur de l'arc et de la corde...

[mathelot]

Bonjour,

R=rayon
A=longueur d'arc
C=corde
= angle au centre en radians







d'où une équation d'inconnue R ou à résoudre par une méthode numérique

si l'angle est petit, on peut remplacer par ce qui donne C=A

[mantus]

oui en fait voila mon probleme
j'arrive a un C=2R sin(A/2R) et je ne sais pas resoudre ce genre de truc
je pensais effectivement qu'il etait possible d'avoir une formule R=machin
mais du coup la j'suis un peu perdu :)

[Ben314]

En reprenant les notations de mathelot, on a : avec et connus et à déterminer.
Cela revient à .
Arrivé à ce point, tu ne peut pas déduire de la deuxième équation une formule de la forme =quelque chose de simple.
Mais, si tu connais les valeurs numériques de et , en traçant la courbe de , tu peut trouver une valeur approximative de .

[mathelot]

je réfléchis sur la présentation de Ben314 :++:

nous devons tirer partie du fait que la courbe de la fonction
est presque une droite

sur l'intervalle

le graphe étant proche de celui de

[oscar]

Longueur de l' arc AB = R *x ( x est la mesure de l' angle au centre exprimé en radians)
Longueur de la corde AB = 2R sin x/2

[oscar]

figure


http://yfrog.com/1sarcetcorde2j

[mathelot]

re,

on a le développement limité du sinus
en x=0



ce qui revient à approximer la courbe de sin() par un polynôme
pour x proche de 0.

l'intérêt , c'est que l'équation


est une équation trinôme (bicarrée) dont on obtient facilement
une solution

on pose
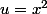et
car la corde est un peu moins longue que l'arc

soit





d'où




comme car

c'est la deuxième solution qui est la bonne

avec

[mathelot]

re,

testons ! y-a-t-il une AN ?

[mantus]

ebein interessant tout ca :)

je crois que c la ou j'ai bloque. je connais pas du tout les developpements limites

sinon pour parler plus precisement du probleme c'est assez simple

en gros on a la distance d'un pont
la largeur de la riviere et il faut calculer la hauteur du pont

j'etais arrive a ce
C/A=sin(a/2)/(a/2)

du coup avec C/A=sin(x)/x
je devrais avoir
a=2x
r=A/a
h=r-r cos(x)