Question suite récurrente
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jklmmlkj
- Membre Relatif
- Messages: 182
- Enregistré le: 15 Sep 2007, 19:13
-
 par jklmmlkj » 09 Jan 2010, 14:18
par jklmmlkj » 09 Jan 2010, 14:18
Bonjours tout le monde, j'ai une petite question, comment montrer que la suite Un est strictement positive pour tout n N :
Un+1 = Un/2 + 1/Un.
Il faut d'abord trouver Un ?
Merci de vos réponses!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Jan 2010, 14:20
par barbu23 » 09 Jan 2010, 14:20
Bonjour : :happy3:
Tu procèdes par récurrence ! :happy3:
Cordialement ! :happy3:
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 09 Jan 2010, 14:23
par wserdx » 09 Jan 2010, 14:23
Tu vois que cette propriété dépend du premier terme de la suite.
As-tu essayé une démonstration par récurrence?
-
jklmmlkj
- Membre Relatif
- Messages: 182
- Enregistré le: 15 Sep 2007, 19:13
-
 par jklmmlkj » 09 Jan 2010, 14:25
par jklmmlkj » 09 Jan 2010, 14:25
Je vais essayer, merci!
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Jan 2010, 14:25
par barbu23 » 09 Jan 2010, 14:25
Oui, mais que vaut

? :hum: :happy3:
-
jklmmlkj
- Membre Relatif
- Messages: 182
- Enregistré le: 15 Sep 2007, 19:13
-
 par jklmmlkj » 09 Jan 2010, 14:33
par jklmmlkj » 09 Jan 2010, 14:33
Pardon, U0 = 2. Effectivement, ca marche par récurrence, mais lorsqu'on demande Un >

sans utiliser la récurrence?
Merci.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Jan 2010, 14:36
par barbu23 » 09 Jan 2010, 14:36
Toujours, par recurrence ! :)
En fait pour demontrer n'importe quelle formule e, fonction de suite, il faut toujours penser à proceder par recurrence ! :happy3:
-
jklmmlkj
- Membre Relatif
- Messages: 182
- Enregistré le: 15 Sep 2007, 19:13
-
 par jklmmlkj » 09 Jan 2010, 14:39
par jklmmlkj » 09 Jan 2010, 14:39
Merci mais dans un examen blanc, il y a : "Démontrer, sans utiliser un raisonnement par récurrence, que pour tout n N, Un >

"
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Jan 2010, 14:48
par barbu23 » 09 Jan 2010, 14:48
Je ne pense pas ! il me semble que c'est impossible mais je ne sais pas ! :happy3:
-
jklmmlkj
- Membre Relatif
- Messages: 182
- Enregistré le: 15 Sep 2007, 19:13
-
 par jklmmlkj » 09 Jan 2010, 14:57
par jklmmlkj » 09 Jan 2010, 14:57
Ben moi je trouve que Un > i

...
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Jan 2010, 15:06
par barbu23 » 09 Jan 2010, 15:06
Il y'a la methode directe qui consiste à resoudre ( comme on fait en equation differnetielle :happy3: ) l'équation :

( je suppose donc, que tu connais cette methode de résolution de suites récurrentes linéaires, comme c'est le cas des equations differnetielles linéaires ) et on finit par trouver une formule explicite à

( par exemple :
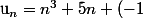^{4n} $)
) et à partir de cette formule, on majore pour arriver à la conclusion que

par exemple ! :happy3:
-
jklmmlkj
- Membre Relatif
- Messages: 182
- Enregistré le: 15 Sep 2007, 19:13
-
 par jklmmlkj » 09 Jan 2010, 15:18
par jklmmlkj » 09 Jan 2010, 15:18
Merci mais comment avoir l'équation

sachant que c'est

.
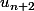
ne vaut pas plutôt :

?
Merci.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 09 Jan 2010, 15:23
par barbu23 » 09 Jan 2010, 15:23
Non, pas ça ! :happy3:
Tu tapes : suite récurrente linéaire sur google, et tu apprends à appliquer l'algorithme sans aucune peine ! :) c'est juste une methode qu'il faut garder à l'esprit comme on fait pour les equations differnetielles linéaires , c'est à peu près la même chose ! :happy3:
-
ffpower
- Membre Complexe
- Messages: 2542
- Enregistré le: 13 Déc 2007, 04:25
-
 par ffpower » 09 Jan 2010, 15:25
par ffpower » 09 Jan 2010, 15:25
sauf que la,c est pas une suite reccurente linéaire...

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 09 Jan 2010, 16:16
par Ben314 » 09 Jan 2010, 16:16
Il suffit d'étudier sur R+ la fonction x->x/2+1/x...
(mais cela ne donne qu'une inégalité large)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 09 Jan 2010, 16:18
par Ben314 » 09 Jan 2010, 16:18
Quand à
jklmmlkj a écrit:Ben moi je trouve que Un > i

...
, je te rapelle qu'il n'y a pas de relation d'ordre (compatible) sur C.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
jklmmlkj
- Membre Relatif
- Messages: 182
- Enregistré le: 15 Sep 2007, 19:13
-
 par jklmmlkj » 09 Jan 2010, 16:21
par jklmmlkj » 09 Jan 2010, 16:21
Ok, merci!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
 ( je suppose donc, que tu connais cette methode de résolution de suites récurrentes linéaires, comme c'est le cas des equations differnetielles linéaires ) et on finit par trouver une formule explicite à
( je suppose donc, que tu connais cette methode de résolution de suites récurrentes linéaires, comme c'est le cas des equations differnetielles linéaires ) et on finit par trouver une formule explicite à  ( par exemple :
( par exemple : 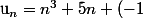^{4n} $) ) et à partir de cette formule, on majore pour arriver à la conclusion que
) et à partir de cette formule, on majore pour arriver à la conclusion que  par exemple ! :happy3:
par exemple ! :happy3: