Nombres complexes

[oméga18]

j'ai vraiment des problèmes pour résoudre même des additions avec l'exponentielle, si quelqu'un pouvait m'expliquer rien qu'un exo je pourrais faire le reste :/
Voilà quelques énoncés :

1) faire z1*z2 et z1+z2
z1=2e(2i(pi)/3) ; z2=(racine de 2)e(i(pi)/4)
z1=2e(i(pi)/2) ; z2=2e(-i(pi)/3)

2) mettre sous forme cartésienne (là c'est la puissance qui me bloque)
2e(2i(pi)/3 ; e(5i(pi)/6)

Et pour placer un complexe dans le plan, j'ai compris quand j'ai la forme cartésienne comme (1 + i) mais avec l'exponentielle je ne sais pas comment faire :
2e(i(pi)/3) ; -e(2i(pi)/3)

Merci d'avance :)

[dudumath]

que trouves-tu pour z1*z2? qu'est ce qui te gène dans la multiplication et l'addition de complexes?

[oméga18]

en fait déjà mon gros problème c'est surtout l'addition ici, parce que je pense qu'il faut remettre en écriture cartésienne et je n'y arrive pas avec le 2iPI/3 par exemple, en fait moi je croyais que c'était égale a 2PI/3 mais ça ne tombe pas sur le bon résultat donc je dois avoir tort lol

[mathelot]

Bonsoir,

les nombres complexes sont les affixes des points du plan. C'est le mathématicien suisse Argand , qui a eu l'idée,le premier, d'associer un complexe et un point.

Un nombre complexe, c'est donc deux coordonnées à la fois en un seul nombre !

ensuite, on pose


d'une part, ces exponentielles sont les nombres complexes de module 1,
ce que l'on voit avec la série entière qui définit exp(z)

de
on en déduit que

d'autre part, le fait que exp() soit un morphisme de R,+ sur U permet de définir la mesure des angles orientés de vecteurs par les arcs du cercle
de rayon 1.

On peut donc placer le point M d'affixe grâce au réel 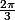qui mesure l'angle

remarque si l'on songe aux différents enchainements de démonstration,
entre celle de la propriété exp(z+z')=exp(z).exp(z'),
et les mesures d'angles associées aux matrices de rotation, on sent que la possibilité de mesurer une rotation, un "mouvement tournant" découle,in fine, des bonnes propriétés du triangle de Pascal et des coefficients binomiaux.

[oméga18]

oui mais moi quand je fais passer en cartésien, et après le nombre cartésien si je le refait passer en trigo, ça ne marche plus je ne trouve plus le bon module ni argument donc ma méthode doit être mauvaise, et j'en aurai voulu une qui marche.
Et pour placer un point dans le plan, il faut absolument que je repasse en cartésien ou je peux le faire directement avec l'expo ?

[mathelot]

oui mais moi quand je fais passer en cartésien, et après le nombre cartésien si je le refait passer en trigo, ça ne marche plus

coordonnées cartésiennes vers coordonnées polaires



polaires vers cartésiennes

Et pour placer un point dans le plan, il faut absolument que je repasse en cartésien ou je peux le faire directement avec l'expo ?

directement avec l'expo.

[oméga18]

non mais par exemple je fais passer :

or module de z :
r = 4 et non pas 2 comme au départ, en revanche l'arguement je crois que c'est bon mais pas sûr.

Et ensuite pour faire directement par l'expo, je dois carrément faire avec l'angle ? et le module la longueur du vecteur ? ou autrement ? parce que je trouve que c'est bof comme méthode.

(déjà merci)

[mathelot]

non mais par exemple je fais passer :
2e(2iPI/3) = 2(cos 2PI/3 +i sin 2PI/3) = 2 + 2i (racine de 3) = z
or module de z :
r = 4 et non pas 2 comme au départ

4 est le carré du module

Et ensuite pour faire directement par l'expo, je dois carrément faire avec l'angle ? et le module la longueur du vecteur ?

bah oui. on utilise le cercle

[oméga18]

Aaaaaaaaah argument fois 2 et module au carré okaaaaaaay j'ai compris !!
Merci beaucoup :)