Derivation

[neo62950]

bonjour
je solicite votre aide car je dois derivé une fonction mais je ne suis pas sur du resultat



pour l'instant moi j'ai fait:

u= 1+x donc u'=1
v=1-x donc v'=1



ensuite (f°g)'= (f'°g)g'

soit (f°g)'=

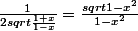
Voila donc dites mois ske vous en penser (tre pratique mais tres long la balise tex)

[le_fabien]

bonjour
je solicite votre aide car je dois derivé une fonction mais je ne suis pas sur du resultat



pour l'instant moi j'ai fait:

u= 1+x donc u'=1
v=1-x donc v'=1



ensuite (f°g)'= (f'°g)g'

soit (f°g)'=

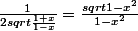
Voila donc dites mois ske vous en penser (tre pratique mais tres long la balise tex)

Bonjourr,
beaucoup d'erreurs. :we:

[neo62950]

je me doute que j'ai fait des erreurs car je n'ai jamais fait ce genre de derivation mais pouvais vous me dire ou j'ai fait des erreur

[oscar]

Bjr
u = x+1 et v = x-1
(u/v)'= 2/ ( x-1)²

[V (x+1)/ ( x-1)]' =( 1/ (x-1)²) / v(x+1)/(1-x)= 1 / (x-1))² v (x+1)/(x-1) =

[neo62950]

mince desolé mais au debut c 'est 1+x/1-x qui est sous la racine et non x+1/x-1

[neo62950]

voila le changement est fait

[le_fabien]

bonjour
je sollicite votre aide car je dois deriver une fonction mais je ne suis pas sur du résultat



pour l'instant moi j'ai fait:

u= 1+x donc u'=1
v=1-x donc v'=1



ensuite (f°g)'= (f'°g)g'

soit (f°g)'=

Voila donc dites moi ce que vous en pensez (trés pratique mais trés long la balise tex)

Voilà le changement est fait. :zen:

[mito94]

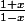
moi ce que je fait c'est que je pose tout . tout d'abord je fais la dérivée de en posant A' et B' si tu as pas labitude encore de les faires de tete . puis aprés tu pose la formule des dérivées composees.
u'(x)*v'(u(x)

[neo62950]

ok merci bien

[neo62950]

ha ok ok se qui, en simplifiant, me donne