Nombres complexes

[cchm]

Bonjour à tous,

J'aurai besoin de votre aide pour un exercice sur les complexes



Dans le plan complexe rapporté à un repère orthonormal direct (O, u, v), on considère l'application f du plan dans lui même qui, à tout point M d'affixe z associe le point M' d'affixe z' tel que:

z'=z²-4z

1 - On suppose que deux points ont la même image par f, démontrer qu'ils sont confondus ou que l'un est l'image de l'autre par une symétrie centrale que l'on précisera


2 - Soit I le point d'affixe -3.

Démontrer que OMIM' est un parallélogramme si et seulement si z²-3z+3=0



Merci d'avance

[mathelot]

bonjour,

soient deux images égales, et
ce sont des images, qui proviennent d'antécédents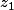 et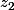

égaliser
et se ramener à une équation produit nul .
ça donne comme solution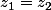 ou ...

2)
traduire la condition "avoir les deux diagonales qui se coupent en leur milieu"
en une égalité portant sur les affixes des sommets du quadrilatère

[cchm]

Merci pour cette réponse rapide.

En effet, j'avais déjà posé comme condition






Mais que mettre en facteur pour arriver à une équation de produit nul, sachant que nous avons ici deux inconnues ?

[Ericovitchi]

et là on voit bien que ou bien ou une symétrie ?

[cchm]

z1 et z2 ont même image, donc:

z







C'est donc bon pour la factorisation

Donc

ou

Est-ce juste?


Edit: Merci Ericovitchi pour cette réponse

[Ericovitchi]

oui mais il faut que tu précises de quelle "symétrie centrale" il s'agit exactement.
si , par quelle symétrie M' se déduit t-il de M ?

[cchm]

La symétrie est définie par l'expression des affixes sous la forme



Soit

Donc une symétrie de centre I d'affixe 2?

[cchm]

J'ai terminé cet exercice, merci à tous pour votre aide.

Bonne journée