Bonjour,
Je vous écris car je n'arrive pas a comprendre la résolution d'un programme ou plus précisément d'une matrice.
Par exemple, comment à partir de la fonction suivante :
maximiser f(x1, x2) = 5x1 + 5x2 - x1^2-x2^2 = cx - 1/2 (tx)Qx
où (tx) est la transposé de x.
à partir de cette fonction j'aimerai juste savoir comment on arrive à trouver la matrice suivante:
Q = ( 2 0
0 2 )
Amicalement.
Programme quadratique
2 messages
- Page 1 sur 1
salut,
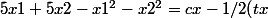Qx)
la premiere chose a faire, c'est d'isoler les termes qui sont de degré 2, genre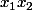 , et
, et  et
et .
.
Dans cx, tu auras donc du x1, et du x2.
Ensuite, avec ces termes de "degré 2", tu peux placer dans ton Q le coeff correspondant a et le coeff correspondant a
et le coeff correspondant a  sur la diagonale de ton Q.
sur la diagonale de ton Q.
Quand tu vas developper,
 , avec
, avec 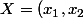') tu auras dans
tu auras dans ) le coeff correspondant a
le coeff correspondant a  , de même dans
, de même dans ) le coeff correspondant a
le coeff correspondant a  .
.
Ensuite, pour les termes en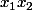 , ils sont exprimés deux fois quand tu développes.
, ils sont exprimés deux fois quand tu développes.
La premiere fois : , et la deuxieme fois :
, et la deuxieme fois :  .
.
L'idée c'est de prendre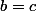 , et b+c=le coeff pour le terme en
, et b+c=le coeff pour le terme en 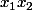 . avec b et c des scalaires du Q.
. avec b et c des scalaires du Q.
Ainsi, tu as une matrice symétrique.
Essaie decrire la matrice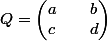 et de developper
et de developper  , ca peut aider
, ca peut aider
(ici comme tu nas pas de terme en x_1x_2, b et c valent 0)
edit: apres faut faire gaffe au demi facteur devant ton Q, mais ca s'ajuste.
PS : dsl pour la subtilité.
la premiere chose a faire, c'est d'isoler les termes qui sont de degré 2, genre
Dans cx, tu auras donc du x1, et du x2.
Ensuite, avec ces termes de "degré 2", tu peux placer dans ton Q le coeff correspondant a
Quand tu vas developper,
Ensuite, pour les termes en
La premiere fois :
L'idée c'est de prendre
Ainsi, tu as une matrice symétrique.
Essaie decrire la matrice
(ici comme tu nas pas de terme en x_1x_2, b et c valent 0)
edit: apres faut faire gaffe au demi facteur devant ton Q, mais ca s'ajuste.
PS : dsl pour la subtilité.
la vie est une fête 
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 200 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
