Problème d'optimisation ...
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
luly
- Membre Naturel
- Messages: 25
- Enregistré le: 25 Jan 2009, 13:43
-
 par luly » 24 Mai 2009, 14:22
par luly » 24 Mai 2009, 14:22
Bonjour !
J'ai un peu de mal avec le problème suivant :
On doit construire une clotûre qui a la forme d'un triangle rectangle, dont l'hypoténuse vaut 80 mètres. Il faut que le terrain délimité par la clotûre ait la plus grande aire possible.Pour l'instant j'ai ceci :

Aire =

=

En remplaçant c² par b², cela me donne au final :
}{2})
De là, il faut calculer la dérivée, et c'est là que je bloque, parce que mes calculs sont erronés. Alors, une petite idée ? :hein:
Merci d'avance !
-
Cheche
- Membre Rationnel
- Messages: 650
- Enregistré le: 17 Avr 2009, 19:25
-
 par Cheche » 24 Mai 2009, 14:33
par Cheche » 24 Mai 2009, 14:33
Salut,
Ton raisonnement se tient très bien.
Mais j'aimerai que tu reprennes ton expression de l'aire du triangle.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 24 Mai 2009, 14:36
par Ericovitchi » 24 Mai 2009, 14:36
Pourquoi

?
j'aurais plutôt mis

?
-
luly
- Membre Naturel
- Messages: 25
- Enregistré le: 25 Jan 2009, 13:43
-
 par luly » 24 Mai 2009, 14:58
par luly » 24 Mai 2009, 14:58
Ha oui, je ne l'avais pas vu ainsi.
Ca nous donnerait :
}{2} = 64000-40b^2)
Et la dérivée : -80.b
b vaut 0 alors :hein: ?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 24 Mai 2009, 15:14
par Ericovitchi » 24 Mai 2009, 15:14
Heu, j'ai du mal à te suivre.
l'aire vaut bc/2
et comme

fais b= .... et remplaces
et déjà tu auras une formule donnant l'aire un peu plus exacte.
-
luly
- Membre Naturel
- Messages: 25
- Enregistré le: 25 Jan 2009, 13:43
-
 par luly » 24 Mai 2009, 16:20
par luly » 24 Mai 2009, 16:20
Ok, donc :

Jusqu'à maintenant c'est correct ?
 par busard_des_roseaux » 24 Mai 2009, 17:54
par busard_des_roseaux » 24 Mai 2009, 17:54
Bj,
ABM est rectangle en M . L'hypoténuse (fixe) AB vaut 80.
M est donc situé sur un cercle, de diamètre [AB], de rayon R=40.
mézalor, on peut faire de la trigonométrie...

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 24 Mai 2009, 18:09
par Ericovitchi » 24 Mai 2009, 18:09
L'aire c'est bc/2, pourquoi multiplies tu par 80 qui est l'hypoténuse ? je ne comprends pas.
-
luly
- Membre Naturel
- Messages: 25
- Enregistré le: 25 Jan 2009, 13:43
-
 par luly » 24 Mai 2009, 18:33
par luly » 24 Mai 2009, 18:33
Ericovitchi a écrit:L'aire c'est bc/2, pourquoi multiplies tu par 80 qui est l'hypoténuse ? je ne comprends pas.
Je multiplie, comme le dis la formule, la base (qui vaut 80) par la hauteur (c'est un triangle rectangle, donc l'un des deux côtés de l'angle droit) et on divise le tout par deux.

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 24 Mai 2009, 19:07
par Ericovitchi » 24 Mai 2009, 19:07
80 c'est l'hypoténuse.
les deux autres cotés sont b et c
l'aire c'est bc/2. Si tu prend l'hypoténuse comme base, il faut multiplier par la hauteur. Tu la connais comment la hauteur ?

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 24 Mai 2009, 19:26
par Ericovitchi » 24 Mai 2009, 19:26
sinon si tu ne veux pas t'embêter avec des racines, suis la suggestion de notre ami le buzard. Tu prend un cercle de diamètre 80 et tu fais tourner le point M sur le cercle. tu le repère par un angle x.
Ton aire vaut 80 sin x/2 = 40 sinx et il est très facile de voir où est le maximum.
-
luly
- Membre Naturel
- Messages: 25
- Enregistré le: 25 Jan 2009, 13:43
-
 par luly » 24 Mai 2009, 20:05
par luly » 24 Mai 2009, 20:05
Oui, c'est une proposition intéressante. D'ailleurs, en voici une autre :

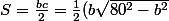)
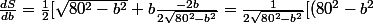-b^2]=<br />\frac{80^2-2b^2}{2\sqrt{80^2-b^2}})

pour

soit pour

et

soit

Merci pour votre aide en tout cas.
Bonne soirée ! :++:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
