Dm fonction polynomes
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
coucou008
- Membre Naturel
- Messages: 18
- Enregistré le: 30 Oct 2008, 20:10
-
 par coucou008 » 02 Nov 2008, 17:17
par coucou008 » 02 Nov 2008, 17:17
MERCI BCP timmm ideal ^^ lol tu m'a beaucoup beaucoup aider et puis même ceux qui m'ont repondu ça ma beaucoup servi merci
coucou008 :++:
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 02 Nov 2008, 17:18
par Timothé Lefebvre » 02 Nov 2008, 17:18
Détail du calcul de l'abscisse du point

, sommet de la parabole :
= \frac{5 \pi}{2} \times { \frac{4}{2 \pi}} = 5)
En fait on multiplie par l'inverse !
PS : de rien ma moitié chérie

-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 02 Nov 2008, 17:41
par Euler911 » 02 Nov 2008, 17:41
Timothé Lefebvre a écrit:Autre détail :
 = \frac{25 \pi^2}{4} \times { \frac{1}{\pi}}= -\frac{25}{4} \pi)
Y sort d'où le " - 25/4"???
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 02 Nov 2008, 17:43
par Timothé Lefebvre » 02 Nov 2008, 17:43
Ah merde t'as raison j'ai mis un moins en trop ^^
Désolé Choup :s
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 02 Nov 2008, 17:52
par Timothé Lefebvre » 02 Nov 2008, 17:52
Je t'explique maintenant le coup du polynôme :
On part de
 = \frac{\pi}{4} (10x - x^2))
En développant on a :
 = \frac{\pi}{4}x^2 - \frac{5 \pi}{2}x)
Le polynôme du seconde degré s'écrit de la forme
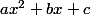
, ici

,

et
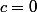
.
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 02 Nov 2008, 18:55
par Timothé Lefebvre » 02 Nov 2008, 18:55
Pour s'amuser un peu, on va calculer les racines de ce polynôme.
On a

.
De plus,
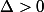
, on a donc deux racines,

et

.


Et,



-
coucou008
- Membre Naturel
- Messages: 18
- Enregistré le: 30 Oct 2008, 20:10
-
 par coucou008 » 02 Nov 2008, 19:05
par coucou008 » 02 Nov 2008, 19:05
MERCI TIM :p mais

n'est pas egal à

???
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 02 Nov 2008, 19:08
par Timothé Lefebvre » 02 Nov 2008, 19:08
Si tout à fait pourquoi ?!
J'ai réduis direct, j'y suis peut-être allé trop ?
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 03 Nov 2008, 21:38
par Timothé Lefebvre » 03 Nov 2008, 21:38
Coucou chérie

Alors comme promis je te détaille plus l'expression qu'on avait trouvée je ne sais plus quand.
On a donc :
 = \frac{1}{2} \pi (\frac{10}{2})^2 - \frac{1}{2} \pi (\frac{x}{2})^2 - \frac{1}{2} \pi (\frac{10-x}{2})^2)
 = -\frac{1}{8} \pi x^2 - \frac{1}{8} \pi (10 - x)^2 + \frac{1}{8} \pi(10^2))
 = -\frac{1}{8} \pi (x^2 + (10-x)^2 - 10^2))
 = -\frac{\pi}{8}(x^2 + 10^2 -20x + x^2 - 10^2))
 = -\frac{\pi}{8}(2x^2 -20x))
 = -\frac{\pi}{4}(x^2-10x))
Voilà, ça c'est le polynôme sous sa forme canonique !
Sous forme développée on aura :
 = -\frac{\pi}{4}x^2 -\frac{5 \pi}{2}x)
Voili voilou :lettre: (cool ce smiley, t'en penses quoi ?!)
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 03 Nov 2008, 21:41
par Euler911 » 03 Nov 2008, 21:41
Salut!
Timothé Lefebvre a écrit: = \frac{1}{2} \pi (\frac{10}{2})^2 - \frac{1}{2} \pi (\frac{x}{2})^2 - \frac{1}{2} \pi (\frac{10-x}{2})^2)
 = -\frac{1}{8} \pi x^2 - \frac{1}{8} \pi (10 - x)^2 + \frac{1}{8} \pi(10^2))
 = -\frac{1}{8} \pi (x^2 + (10-x)^2 - 10^2))
 = -\frac{\pi}{8}(x^2 + 10^2 -20x + x^2 - 10^2))
 = -\frac{\pi}{8}(2x^2 -20x))
 = -\frac{\pi}{4}(x^2-10x))
J'ai fais ça non??;)
Voilà, ça c'est le polynôme sous sa forme canonique !
En es-tu certains?
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 03 Nov 2008, 21:56
par Timothé Lefebvre » 03 Nov 2008, 21:56
Tu l'avais écris ?! Ah mince désolé :s
Oui je crois bien ^^ Enfin c'est comme ça que je l'appelle, tu l'appelerais factorisée toi c'est ça ?
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 03 Nov 2008, 22:01
par Euler911 » 03 Nov 2008, 22:01
Timothé Lefebvre a écrit:Tu l'avais écris ?! Ah mince désolé :s
Oui je crois bien ^^ Enfin c'est comme ça que je l'appelle, tu l'appelerais factorisée toi c'est ça ?
Pas vraiment factorisée puisque l'on peut encore mettre x en évidence. Mais surtout pas forme canonique!
Par définition la forme canonique d'un polynôme du second degré est:
^2-\frac{\rho}{4a^2}\right])
Où

est le discriminant du polynôme.
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 03 Nov 2008, 22:02
par Timothé Lefebvre » 03 Nov 2008, 22:02
Ah bon :doh:
Regarde mon expression et la forme canonique, elles sont pareilles ! Le facteur, le carré, la soustraction !
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 03 Nov 2008, 22:03
par Euler911 » 03 Nov 2008, 22:03
Timothé Lefebvre a écrit:Ah bon :doh:
Regarde mon expression et la forme canonique, elles sont pareilles ! Le facteur, le carré, la soustraction !
Je dois être aveugle parce que je ne vois pas la même chose...
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 03 Nov 2008, 22:05
par Timothé Lefebvre » 03 Nov 2008, 22:05
Lol ouais sans doute ! Alors quelle serait la forme canonique de ce polynôme très cher Euler911 ^^ ?
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 03 Nov 2008, 22:10
par Euler911 » 03 Nov 2008, 22:10
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 03 Nov 2008, 22:12
par Timothé Lefebvre » 03 Nov 2008, 22:12
Euler911 a écrit:&=&\frac{-\pi}{4}\left(x^2-10x+25-25\right)\\<br />&=&\frac{-\pi}{4}\left[\left(x-5\right)^2-25\right]\end{eqnarray})
Et si à la fin de ta première ligne on faisait

?
-
Euler911
- Membre Irrationnel
- Messages: 1486
- Enregistré le: 15 Aoû 2008, 17:14
-
 par Euler911 » 03 Nov 2008, 22:13
par Euler911 » 03 Nov 2008, 22:13
Timothé Lefebvre a écrit:Et si à la fin de ta première ligne on faisait

?
Le +25-25 est fait exprès... c'est une astuce de calcul pour arriver à l'expression canonique de A(x)
-
Timothé Lefebvre
- Membre Légendaire
- Messages: 12478
- Enregistré le: 14 Déc 2005, 12:00
-
 par Timothé Lefebvre » 03 Nov 2008, 22:19
par Timothé Lefebvre » 03 Nov 2008, 22:19
Bon bon si tu le dis ^^
PS : ma Chpou's va faloir que tu décides comment tu préfères l'appeler cette forme ^^
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 44 invités
