Dm fonction polynomes
66 messages
- Page 2 sur 4 - 1, 2, 3, 4
Re chérie,
bon ben je cherche toujours ce truc, faudrait que tu me files l'exo complet tout à l'heure pour que je vois si il n'y a pas un truc qui m'a échappé.
Je crois d'ailleurs qu'il y a un soucis dans le développement d'Yvelines78, mais il faut que je re-vérifie.
A toute, quand tu te réveilleras :D
bon ben je cherche toujours ce truc, faudrait que tu me files l'exo complet tout à l'heure pour que je vois si il n'y a pas un truc qui m'a échappé.
Je crois d'ailleurs qu'il y a un soucis dans le développement d'Yvelines78, mais il faut que je re-vérifie.
A toute, quand tu te réveilleras :D
Timothé Lefebvre a écrit:Eh bien je t'explique :est d'environ 123 c'est possible, jusque là pas de problème, par contre si a < 0 comme c'est le cas ici alors ça veut dire que la parabole sera tournée vers le bas et qu'il n'y a pas de racine réelle ... Bizarre tout ça ...
Si le déterminant d'un polynôme du second degré est strictement positif, il y a d'office deux zéros distincts! Peu importe le signe de a.
Euler911 a écrit:Si le déterminant d'un polynôme du second degré est strictement positif, il y a d'office deux zéros distincts! Peu importe le signe de a.
Je suis désolé, j'avais oublié le - dans -123, j'ai bien trouvé comme Choup pour le discriminant, en sachant qu'on est parti tous les deux du polynôme d'Yvelines78.
yvelines78 a écrit:bonjour,
t(x)=25pi/2 - pix²/8 - (pi/2)(10-x/2)²
t(x)=25pi/2 - pix²/8 - (pi/2)(100-10x+x²/4)
t(x)=25pi/2 - pix²/8 - 100pi/2 + 5pix - pix²/8
t(x)=-2pix²/8 + 5pix -75pi/2
t(x)=25pi/2 - pix²/8 - (pi/2)(100-20x+x²/4)
t(x)=(pi/2)(25 - x²/4 - 25+20/4x-x²/4)
t(x)=(pi/8)(100-x²-100+20x-x²)
t(x)=(pi/4)(10x-x²)
Re :we:
Alors, question a : la réponse était presque donnée par Euler911, je la développe donc pour en arriver à une forme canonique.
 = \frac{1}{2} \pi (\frac{10}{2})^2 - \frac{1}{2} \pi (\frac{x}{2})^2 - \frac{1}{2} \pi (\frac{10-x}{2})^2)
A(x) = [développement et réduction ...]
 = - \frac{\pi}{4} (x^2 - 10x))
Voilà pour la question a.
Ensuite, pour la question b on veut calculer les coordonnées du sommet de la parabole, on connaît la formule
de la parabole, on connaît la formule ) .
.
Calcul du discriminant :
:
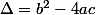
^2)

Ensuite, on va donc calculer les coordonnées du sommet S selon la formule précédente :
= 5)
 = \frac{25}{4} \pi)
Voilà, on a donc en maximum x = 5, et si on replace ça dans le contexte, si x = 5 alors M est le milieu de AB !
Voili voilou :we:
EDIT : il est aussi possible de trouver le maximum par le calcul de dérivée ...
Alors, question a : la réponse était presque donnée par Euler911, je la développe donc pour en arriver à une forme canonique.
A(x) = [développement et réduction ...]
Voilà pour la question a.
Ensuite, pour la question b on veut calculer les coordonnées du sommet
Calcul du discriminant
Ensuite, on va donc calculer les coordonnées du sommet S selon la formule précédente :
Voilà, on a donc en maximum x = 5, et si on replace ça dans le contexte, si x = 5 alors M est le milieu de AB !
Voili voilou :we:
EDIT : il est aussi possible de trouver le maximum par le calcul de dérivée ...
66 messages
- Page 2 sur 4 - 1, 2, 3, 4
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
