Bonjour à tous !
Notre prof de math nous a donné un exo qui est vraiment très hard ^^ ! Ca fait depuis hier que j'essaye de le faire mais pas moyen ... J'espere que vous pourrez m'eclairer un peu ;) :
f est une fonction définie et continue sur un intervallle I. a et b sont dexu réels de I tels que a inferieur a b et k un reel copris entre f(a) et f(b). On suppose que k est compris entre f(a) et f(b). On contruit ci dessous par recurrence :
-Une suite croissante (an) telle que pour tout n de N, f(an) inferieur ou egale a k.
-Une suite decroissante (bn) telle que pour tout n de N, k inferieur ou égal a f(bn).
On pose a0= a et b0=b. On suppose contruits les thermes des deux suites jusqu'au rang n.
Si f((an+bn)/2) inferieur ou égal a k, on pose an+1= (an+bn)/2 et bn+1=bn
Si f((an+bn)/2) superieur strictement a k, on pose an+1=an et bn+1= (an+bn)/2.
1/ a)Verifier que la suite (an) est croissante et que la suite (bn) est decroissante.
b)Demontrez que pour tout n de N, bn-an=1/2^n(b0-a0)
c)En déduire que les suites (an) et (bn) sont adjacentes. On note c leur limite comune.
2/ a)Quelle est la limite de f(an) et de f(bn) lorque n tends vers + l'infini ? Justifier le resultat.
b)Terminer la demonstration du theoreme des valeurs intermiediaires.
Voili Voilou . J'en suis toujours au point 0 ... Merci de m'eclaireer ;)
Exo T°S Fonction
13 messages
- Page 1 sur 1
Salut !
T'as de la chance, j'ai justement un DS en partie là-dessus mercredi alors du coup je l'ai fait :
Pour la question 1) a) : j'ai prouvé par récurrence que pour tout n, b_n >= a_n. Ceci fait, on prouve facilement, encore une fois par récurrence, que pour tout n a_n+1 >= a_n et que b_n+1 =< b_n
Pour la question b) : c'est encore une récurrence, en étudiant d'abord ce qui se passe dans le cas 1 (Si f((an+bn)/2) =< k) puis dans le cas 2
enfin, pour la question c) c'est immédiat après avoir trouvé le b)
Voilà pour la question 1), je vais manger et je fais la suite après.
Dis-moi si tu as besoin de plus d'indices :++:
T'as de la chance, j'ai justement un DS en partie là-dessus mercredi alors du coup je l'ai fait :
Pour la question 1) a) : j'ai prouvé par récurrence que pour tout n, b_n >= a_n. Ceci fait, on prouve facilement, encore une fois par récurrence, que pour tout n a_n+1 >= a_n et que b_n+1 =< b_n
Pour la question b) : c'est encore une récurrence, en étudiant d'abord ce qui se passe dans le cas 1 (Si f((an+bn)/2) =< k) puis dans le cas 2
enfin, pour la question c) c'est immédiat après avoir trouvé le b)
Voilà pour la question 1), je vais manger et je fais la suite après.
Dis-moi si tu as besoin de plus d'indices :++:
D'accord, alors pour la b), tu prouves que P_0 est vraie. ce qui se fait en disant que (1/2)^0 = 1
Ensuite, tu supposes Pn vraie, et tu cherches si Pn+1 vraie.
Dans le cas 2 : tu as : b_n = (a_n+b_n) / 2 et a_n+1 = a_n
Donc tu as : b_n+1 - a_n+1 = ((a_n+b_n) / 2) - a_n
en mettant tout au même dénominateur : b_n+1 - a_n+1 = (b_n - a_n) /2
Or, on a supposé Pn vraie, donc ça veut dire quoi pour b_n-a_n ?
Je te laisse finir le cas 2 et faire ensuite le cas 1
Ensuite, tu supposes Pn vraie, et tu cherches si Pn+1 vraie.
Dans le cas 2 : tu as : b_n = (a_n+b_n) / 2 et a_n+1 = a_n
Donc tu as : b_n+1 - a_n+1 = ((a_n+b_n) / 2) - a_n
en mettant tout au même dénominateur : b_n+1 - a_n+1 = (b_n - a_n) /2
Or, on a supposé Pn vraie, donc ça veut dire quoi pour b_n-a_n ?
Je te laisse finir le cas 2 et faire ensuite le cas 1
Bon alors pour le cas 2, je reprends où j'en étais :
b_n+1 - a_n+1 = (b_n - a_n) /2
Je l'écris en clair pour que tu vois meiux :

Or, on a supposé Pn vraie. et Pn c'était :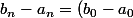\frac{1}{2^n})
Donc on a :
\frac{1}{2^n}}{2} = (b_0-a_0)\frac{1}{2^{n+1}})
C'est à dire, P_n+1..
Pour le cas 1, tu fais pareil et normalement si tu fais pas d'erreur de signe tu te retrouves encore un fois avec :
b_n+1 - a_n+1 = (b_n - a_n) /2
Je l'écris en clair pour que tu vois meiux :
Or, on a supposé Pn vraie. et Pn c'était :
Donc on a :
C'est à dire, P_n+1..
Pour le cas 1, tu fais pareil et normalement si tu fais pas d'erreur de signe tu te retrouves encore un fois avec :
Ok ! ^^ Cette fois j'ai compris une bonne fois pour toute ^^ Je ne savais pas trop comment faire au moment de ((bo-ao)1/2^n)/2 . Maintenant ca va !
Et j'ai revu mon cas 1 et ma faute c'était que j'avais mis : bn+1-an+1 = bn - ((an +bn)/2) et donc egale a (bn -an -bn)/2 alors que non ^^ C'est : (2bn - an - bn)/2 ! :stupid_in ^^ Bref ! Donc la question c) facile en déduire avec les propriété d'une suite adjacente : l'une croissante l'autre decroissante et limite de (an -bn) = 0 et aussi an inferieur ou egale a bn.
Maintenant reste le probleme de la question 2 ou tu as tenté de m'eclairer :p mais je n'ai pas su faire ... ^^
Merci en tout cas pour ton aide ;)
Et j'ai revu mon cas 1 et ma faute c'était que j'avais mis : bn+1-an+1 = bn - ((an +bn)/2) et donc egale a (bn -an -bn)/2 alors que non ^^ C'est : (2bn - an - bn)/2 ! :stupid_in ^^ Bref ! Donc la question c) facile en déduire avec les propriété d'une suite adjacente : l'une croissante l'autre decroissante et limite de (an -bn) = 0 et aussi an inferieur ou egale a bn.
Maintenant reste le probleme de la question 2 ou tu as tenté de m'eclairer :p mais je n'ai pas su faire ... ^^
Merci en tout cas pour ton aide ;)
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 173 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
