Produit scalaire

[roper]

soit f,g C1([0,1], )
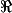
soit le produit scalaire P(f,g)=f(0)g(0)+ f'(t)g'(t)dt

l'intregrale est lineaire donc P est bilineaire est symetrique

P(f,f)=f(0)^2)+ f'(t)^2dt 0
donc P est positif

P(f,f)=0 f(0)^2)+ f'(t)^2dt=0
est ce qu'on peut ecrire f(0)^2)=0 car lineaire ? et en deduire que
f'(t)^2dt=0
f'(t)^2 fonction continue et positive dons c'est la fonction nulle doc f est la fonction nulle

[legeniedesalpages]

Salut,

rien ne nous dit que f est linéaire. On sait juste qu'elle est continûment différentiable.

[yos]

est ce qu'on peut ecrire f(0)^2)=0 car lineaire ? et en deduire que
f'(t)^2dt=0

Non! Mais si une somme de deux nombres positifs vaut 0 alors...