Derivation

[GTO59]

1.soit I=]0;+oo[ et u et v les deux fonctions définies sur I par u(x)=2x-1 et v(x)=
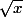
a) montrer que u et v sont derivable sur I et determiner leur derivée.
b) soit f la fonction definie sur I par f(x)=(2x-1)
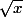
Montrer que f est dérivable sur I
je narrive pas a montrer que u et v sont derivabl et f est derivable on ma parler du tu de variation mais avec quel nombre

[Clembou]

1.soit I=]0;+oo[ et u et v les deux fonctions définies sur I par u(x)=2x-1 et v(x)=
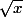
a) montrer que u et v sont derivable sur I et determiner leur derivée.
b) soit f la fonction definie sur I par f(x)=(2x-1)
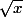
Montrer que f est dérivable sur I
je narrive pas a montrer que u et v sont derivabl et f est derivable on ma parler du tu de variation mais avec quel nombre

Tu appliques le taux de variation pour les points dans I.
Comme alors

et existent car sont définis dans I.

Pour f dérivable, tu dis que c le produit de deux fonctions dérivables donc dérivable.

[GTO59]

je te remercie pour ton aide mais je n'ai pas bien saisi le
ce ne sont pas les derivé de u(x) et v(x)?