Bonjour !
Voila l'énoncé d'un exercice ou j'ai un peu de mal :
f est la fonction définie sur [0;+infini[ par :
f(x) = (2xracine de x)/(1+x)
1. Démontrer que la fonction f est derivable en x=0.
2. Calculer f'(x) pour tout x de ]0;+infini[.
3.a. Demontrer que l'equation f(x)=3 admet une solution unique a dans [0;+infini[.
b. Trouver un encadrement d'amplitude 10^puissance-2 de a.
Pour la dérivée j'ai trouvé (racine de x - x racine de x)/(1+x)² Est-ce juste ?
Et pour le reste je galère... :--:
Merci !
Derivation...
13 messages
- Page 1 sur 1
re,
tu n'as pas vu ce qui suit:
la fonction f , est derivable en xo, sssi, le taux d'accroissement (ou taux de variation)
+f(x_0)}{h}=\frac{f(x)-f(x_0)}{x-x_0}) tend vers une limite finie lorsque h tend vers 0 (cad lorsque x tend vers xo).cette limite est le nombre derivé
tend vers une limite finie lorsque h tend vers 0 (cad lorsque x tend vers xo).cette limite est le nombre derivé
}=\lim_{h\to0}\frac{f(x_0+h)+f(x_0)}{h}=\lim_{x\to{x_0}}\frac{f(x)-f(x_0)}{x-x_0})
pour ton exo
}=\frac{2x\sqrt{x}}{1+x})
donc
}=0)
soit
-f(0)}{x-0}=\frac{f(x)}{x}=\frac{2\sqrt{x}}{x+1})
or
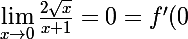)
donc f est derivable en 0 et f'(0)=0
je pense que si tu as une question de ce genre tu as dû voir le nombre derivé en cours
tu n'as pas vu ce qui suit:
la fonction f , est derivable en xo, sssi, le taux d'accroissement (ou taux de variation)
pour ton exo
donc
soit
or
donc f est derivable en 0 et f'(0)=0
je pense que si tu as une question de ce genre tu as dû voir le nombre derivé en cours
En effet j'ai etudié tout ce qui est nombre dérivé, mais mon prof ne nous a parlé de limites que très rapidement, sans nous expliquer réellement ce que c'était (il a dit qu'on verrait ca plus tard).
Sinon merci pour la 1., pourrais-tu m'aider pour la 3 ?
Est ce qu'il faut que je passe le 3 de l'autre coté de manière a obtenir f(x)-3=0 ? Mais après je ne sais pas trop dans quel sens aller...
Sinon merci pour la 1., pourrais-tu m'aider pour la 3 ?
Est ce qu'il faut que je passe le 3 de l'autre coté de manière a obtenir f(x)-3=0 ? Mais après je ne sais pas trop dans quel sens aller...
Re
Bonsoir.
Je suis nouveau sur ce forum mathématique(découvert grace à notre moteur de recherche préféré google )
Bon, j'essai(ça fait quelques années que j'ai arrété les études :doh: )
=\frac{2x\sqrt{x}}{1+x})
1) Il s'agit d'étudier :-f(x_0}{x-x_0})
Ici :
En 0+, cette limite vaut : 0+ ;En 0-, cette limite vaut 0+
On en conclut que la limite en 0+ est égale à celle en 0- donc que la limite en 0 vaut 0+, d'où f est dérivable en 0.
2) Pour ma part, j'ai=\frac{x^2+3x}{(1+x^2)(\sqrt{x})})
3) Th. de la bijection et valeur approchée à la calculatrice
@ +.
Je suis nouveau sur ce forum mathématique(découvert grace à notre moteur de recherche préféré google )
Bon, j'essai(ça fait quelques années que j'ai arrété les études :doh: )
1) Il s'agit d'étudier :
Ici :
En 0+, cette limite vaut : 0+ ;En 0-, cette limite vaut 0+
On en conclut que la limite en 0+ est égale à celle en 0- donc que la limite en 0 vaut 0+, d'où f est dérivable en 0.
2) Pour ma part, j'ai
3) Th. de la bijection et valeur approchée à la calculatrice
@ +.
Re
2x\sqrt{x} est de la forme (uv) et (uv)'=u'v+uv' avec u=2v et v = V(x)
Ici :'=2\sqrt{x]+\frac{x}{\sqrt{x}})
-le th de la bijection : une stricte monotonie sur l'intervalle en question, un ensemble de continuité donc de dérivabilité(tableau de variations conseillé)
++
Ici :
-le th de la bijection : une stricte monotonie sur l'intervalle en question, un ensemble de continuité donc de dérivabilité(tableau de variations conseillé)
++
13 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 175 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
