Valeurs propres d'un endomorphisme

[Engel10]

Salut à tous. Svp je ne comprends pas quelque chose dans la partie hachurée de cet exercice.
En fait je ne comprends pas pourquoi le fait que n-1≤o(a-b) a entrainé que (a-b) est d’ordre n-1. Et qu’est ce qui nous a poussé à savoir qu'ici l’ordre de (a-b) ne peut pas être égal à n .
Merci d'avance!

[Engel10]

Svp j'ai besoin d'aide..

[phyelec]

Je ne connais la notation o(a-b)

mais voilà ce que j'ai remarqué, j'espère que cela va vous apporter des éléments de réponses :

A= aI +b

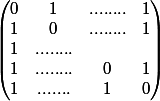
soit A = aI -bI +b

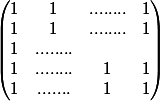
j'appelle U=
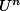
remarque =nU

donc A -(a-b)I= bU donc rg(A -(a-b)I)=rg (bU)

[phyelec]

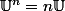
Oups est faux c'est

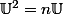
[Engel10]

merci pour ta réponse! Mais la notation o(a-b) signifie l'ordre de multiplicité de la valeur propre a-b.
Depuis ce matin je cherche à comprendre, et ben j'ai viens de comprendre ce qui s'est passé. Merci à tous!

[Rhaegar]

Bonsoir,

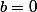
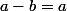
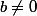
Si , la matrice est diagonale et il est clair que est racine d'ordre n. Si , la matrice remplie de b est de range 1 et donc l'ordre de a-b est n-1. C'est comme ça que je le comprends en tout cas.

[phyelec]

si b=0 det A=
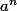
si b différent de 0, en fait, il faut appliquer le théorème du rang (rg(f)+dim(kerf)=dim E ) donc rg(A -(a-b)I)+dim (ker(A -(a-b)I)=n donc dim (ker(A -(a-b)I)=n-1, la multiplicité de la valeur propre (a-b) est n-1,
detA est le produit des valeurs propre. det A= comme la trace Tr(A)=(n-1)(a-b)+ =na , on trouve = a+(n-1)b