
DM de Maths, fonctions dérivée
24 messages
- Page 1 sur 2 - 1, 2
DM de Maths, fonctions dérivée
Bonjour, mon prof de maths m'a donnée ce dm à faire pour les vacances et j'ai du mal à trouver une piste pour commencer l'exercice 1, pouvez-vous me guider svp?


Re: DM de Maths, fonctions dérivée
Bonsoir,
Dans ton cours tu dois avoir appris l'équation d'une tangente à une courbe en un point d'abscisse a ?
Dans ton cours tu dois avoir appris l'équation d'une tangente à une courbe en un point d'abscisse a ?
Re: DM de Maths, fonctions dérivée
triumph59 a écrit:En cliquant sur l'image elle s'affiche en grande taille
ben oui mais je ne sais pas pourquoi ça ne marche pas
sans doute un problème chez moi.
Re: DM de Maths, fonctions dérivée
Pisigma a écrit:Bonjour,
ton scan est illisible
pareil chez moi, quand je zoome , les caractères deviennent flous.
Re: DM de Maths, fonctions dérivée
Bonsoir,
Le problème de la taille de l'image est réglé
Le problème de la taille de l'image est réglé
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: DM de Maths, fonctions dérivée
Bonsoir,
D'après ton cours:
Si est dérivable sur un intervalle contenant
est dérivable sur un intervalle contenant  , alors la tangente à la courbe représentative de
, alors la tangente à la courbe représentative de au point d'abscisse
au point d'abscisse  , a pour équation:
, a pour équation: (x-a)+f(a))
D'après ton cours:
Si
Re: DM de Maths, fonctions dérivée
Oui je comptais partir de l'equation de la tagente mais j'arrive pas à l'exprimer en fonction de la formule de départ
Re: DM de Maths, fonctions dérivée
Bonjour,
Qu'est-ce que tu n'arrives pas à exprimer précisément ?
Dans
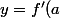(x-a)+f(a))
 et
et  restent les variables de l'équation de la droite, alors que
restent les variables de l'équation de la droite, alors que  est un paramètre. Donc
est un paramètre. Donc
Autrement dit : si on avait dit "tangente au point d'abscisse 0", comment aurait-on fait ? Et si cela avait été "au point d'abscisse 1" ?
Aurélien1608 a écrit:Oui je comptais partir de l'equation de la tagente mais j'arrive pas à l'exprimer en fonction de la formule de départ
Qu'est-ce que tu n'arrives pas à exprimer précisément ?
Dans
- A quoi est égal
?
- A quoi est égal
?
Autrement dit : si on avait dit "tangente au point d'abscisse 0", comment aurait-on fait ? Et si cela avait été "au point d'abscisse 1" ?
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: DM de Maths, fonctions dérivée
Avec l'expression de base qui est f(x) = x² + 2x - 8
Je n'arrive pas a transformer cette expression sous forme y = f'(a)(x-a) + f(a).
En fait j'ai à peine vu la leçon avec mon professeur même si j'ai compris l'ensemble
Je n'arrive pas a transformer cette expression sous forme y = f'(a)(x-a) + f(a).
En fait j'ai à peine vu la leçon avec mon professeur même si j'ai compris l'ensemble
Re: DM de Maths, fonctions dérivée
Il n'y a pas à transformer =x^2+2x-8) en
en 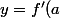(x-a)+f(a)) : cela n'a aucun sens.
: cela n'a aucun sens.
Il faut juste calculer certains termes.
Et tu n'as pas répondu à :
Il faut juste calculer certains termes.
Et tu n'as pas répondu à :
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: DM de Maths, fonctions dérivée
f (a) = a² + 2a - 8
f' (a) = 2a + 2
Je ne suis pas sur pour f' (a), j'ai utilisé les fonctions usuelles
f' (a) = 2a + 2
Je ne suis pas sur pour f' (a), j'ai utilisé les fonctions usuelles
Re: DM de Maths, fonctions dérivée
hdci a écrit:Il n'y a pas à transformeren
: cela n'a aucun sens.
Il faut juste calculer certains termes.
Et tu n'as pas répondu à :
f (a) = a² + 2a - 8
f' (a) = 2a + 2
Je ne suis pas sur pour f' (a), j'ai utilisé les fonctions usuelles
Re: DM de Maths, fonctions dérivée
Bonjour,
Oui c'est ça vous êtes sur la bonne voie:
=x^2+2x-8) donc
donc =a^2+2a-8)
et = 2x+2) donc
donc =2a+2)
Maintenant il faut "injecter" tout ça dans la formule de la tangente
Oui c'est ça vous êtes sur la bonne voie:
et
Maintenant il faut "injecter" tout ça dans la formule de la tangente
Re: DM de Maths, fonctions dérivée
donc j'obtiens y= (2a + 2)(x - a) + a² + 2a - 8
= 2ax - 2a² + 2x - 2a + a² + 2a - 8
= -a² + 2ax + 2x - 8
C'est ça?
= 2ax - 2a² + 2x - 2a + a² + 2a - 8
= -a² + 2ax + 2x - 8
C'est ça?
Re: DM de Maths, fonctions dérivée
Aurélien1608 a écrit:donc j'obtiens y= (2a + 2)(x - a) + a² + 2a - 8
= 2ax - 2a² + 2x - 2a + a² + 2a - 8
= -a² + 2ax + 2x - 8
C'est ça?
Oui ou "presque", il faudrait avoir cela sous la forme y=mx+p donc mettre le x en facteur là où il faut.
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: DM de Maths, fonctions dérivée
Yapuka mettre le 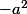 avec le
avec le 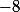 ...
...
Attention, le signe devant a disparu...
a disparu...
Aurélien1608 a écrit:oui donc j'obtiens y = a² + x (2a + 2) - 8
Attention, le signe devant
Il n'y a que 10 types de personne au monde : ceux qui comprennent le binaire et ceux qui ne le comprennent pas.
Re: DM de Maths, fonctions dérivée
Oui erreur d'inatention pour le signe de a², seulement comment mettre -a² et -8 ensemble
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 170 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
