Salut !
1. D'après le cours,
)
est une suite arithmétique de premier terme
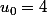
et de raison

donc (toujours d'après le cours) quel que soit l'entier
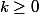
,

. En particulier, si cela est vrai pour un entier
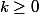
quelconque, cela reste vrai si l'on suppose

compris (au sens large) entre

et

, avec
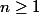
.
2. On obtient alors

égalités :


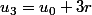
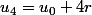
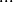
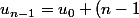r)

Ainsi, si l'on somme membre à membre ces

égalités, on a :
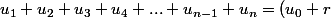+ (u_0+2r)+ (u_0+3r)+ (u_0+4r)+ ... +(u_0+(n-1)r)+ (u_0+nr))
.
3. Dans la somme du membre de droite :
+ (u_0+2r)+ (u_0+3r)+ (u_0+4r)+ ... +(u_0+(n-1)r)+ (u_0+nr))
, on a n termes :

,

,

,

, ...,
r)
et
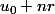
. Dans ces

termes, on a

fois

, et la somme
r+nr)
que l'on peut réécrire (en factorisant par

)
+n)r)
donc :
+ (u_0+2r)+ (u_0+3r)+ (u_0+4r)+ ... +(u_0+(n-1)r)+ (u_0+nr) = nu_0+(r+2r+3r+4r+...+(n-1)r+nr ))
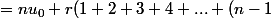+n))
Que vaut en fonction de n la somme
+n)
des

premiers entiers naturels ?
4. Enfin on connait le membre de gauche :

, donc cela te donne :
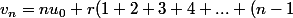+n))
.
Je te laisse faire les calculs et trouver l'expression de v_n en fonction de n.

