Suites géométriques et arithmétiques
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 20 Avr 2012, 03:12
par maths0 » 20 Avr 2012, 03:12
Non !!!

Il y a m-l+1 termes ! (dessus-bas)+1
Ce qui donne, pour n=5 à n=24 combien de termes ?
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
 par Xeniuss » 20 Avr 2012, 03:15
par Xeniuss » 20 Avr 2012, 03:15
Heuu bah 20 termes de 5 à 24
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 20 Avr 2012, 03:17
par maths0 » 20 Avr 2012, 03:17
Oui mais attention pour de l à p on a: p-l+1.
De 5 à 24:

: 20 termes.
De n à p:

: p-n+1 termes.
C'est compris ça ?
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
 par Xeniuss » 20 Avr 2012, 03:18
par Xeniuss » 20 Avr 2012, 03:18
Oui j'ai très bien compris comment sa marche Merci beaucoup!! :)
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 20 Avr 2012, 03:20
par maths0 » 20 Avr 2012, 03:20
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
 par Xeniuss » 20 Avr 2012, 03:33
par Xeniuss » 20 Avr 2012, 03:33
on a donc
 + (\frac {n(n+1)}{2})))
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 20 Avr 2012, 03:34
par maths0 » 20 Avr 2012, 03:34
:mur:
Pour une suite arithmétique, pour faire la somme du premier au dernier:
 Pour une suite géométrique, pour faire la somme du premier au dernier:
Pour une suite géométrique, pour faire la somme du premier au dernier:

(avec q raison de la suite)
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 20 Avr 2012, 03:35
par maths0 » 20 Avr 2012, 03:35

....
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
 par Xeniuss » 20 Avr 2012, 03:38
par Xeniuss » 20 Avr 2012, 03:38
Arithmétique : n+1 x (3+n)/2
Géométrique : 3 x (1-2^n)/(1-q)
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 20 Avr 2012, 03:40
par maths0 » 20 Avr 2012, 03:40
On pourrait vérifier:
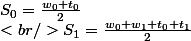
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
 par Xeniuss » 20 Avr 2012, 03:43
par Xeniuss » 20 Avr 2012, 03:43
Ha parce que dans mon cours pour les suites arithmétiques on a la formule
S= (n x (n+1))/2
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 20 Avr 2012, 03:44
par maths0 » 20 Avr 2012, 03:44
D'après la théorie:


Il faut voir à la fin si ça correspond.
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
 par Xeniuss » 20 Avr 2012, 03:49
par Xeniuss » 20 Avr 2012, 03:49
maths0 a écrit:D'après la formule:

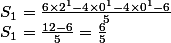
D'après la théorie:




= 6/5 ??
Il faudrait voir si ça correspond.
Oulaa je suis plus trop la :marteau:
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 20 Avr 2012, 03:51
par maths0 » 20 Avr 2012, 03:51
Xeniuss a écrit:Arithmétique : n+1 x (3+n)/2
Géométrique : 3 x (1-2^n)/(1-q)
J'ai localisé l'erreur.
Reprenons là:
d'où tu sors tout ça ?
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
 par Xeniuss » 20 Avr 2012, 03:53
par Xeniuss » 20 Avr 2012, 03:53
c'était d'après les formules que tu ma passé mais je me suis trompé pour la formule de la suite arithmétique :/
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 20 Avr 2012, 03:55
par maths0 » 20 Avr 2012, 03:55
Ce qui donne ? corrige toi.
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
 par Xeniuss » 20 Avr 2012, 03:58
par Xeniuss » 20 Avr 2012, 03:58
La somme de la suite
)
c'est
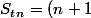 \times \frac {3+(-4n+3)}{2})
puisque le dernier terme est donner par -4n+3
La somme de la suite
)
c'est

-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 20 Avr 2012, 03:59
par maths0 » 20 Avr 2012, 03:59
Le dernier terme est n ! J'avais fais cette erreur !
-
Xeniuss
- Membre Naturel
- Messages: 77
- Enregistré le: 19 Avr 2012, 20:25
-
 par Xeniuss » 20 Avr 2012, 04:02
par Xeniuss » 20 Avr 2012, 04:02
Xeniuss a écrit:La somme de la suite
)
c'est
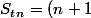 \times \frac {3+(-4n+3)}{2})
puisque le dernier terme est donner par -4n+3
La somme de la suite
)
c'est

Et donc
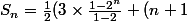 \times \frac {3+n)}{2}))
-
maths0
- Membre Irrationnel
- Messages: 1251
- Enregistré le: 12 Nov 2011, 13:37
-
 par maths0 » 20 Avr 2012, 04:05
par maths0 » 20 Avr 2012, 04:05
Il faut développer et vérifier.

et

(formule de Un donnée dans l'énoncée)
Il faut voir à la fin si ça correspond avec la formule développée.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 72 invités