Suites géométriques et arithmétiques

[maths0]

Où est-ce que tu veux t'arrêter ? t'en es où ?

[Xeniuss]

Nous sommes à l'exercice 2.
J'ai dis n'importe quoi au dessus alors ...
Tu as réussi à prouver l'égalité ?

Voila donc pour revenir a l'exercice 2 j'en était a la question 3)
et je sais pas où me mène mon calcul..

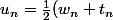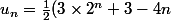[maths0]

Démontrer que !! Tu pars trop loin, reviens !

[Xeniuss]

Démontrer que !! Tu pars trop loin, reviens !

Voila c'est sa mon problème :/
je calcul sa vite fait et je te montre ce que j'ai fait

[maths0]

???
CQFD

[Xeniuss]

???
CQFD

Ha ok.............
j'ai calculé et je tombe sur des calcul monstrueux :mur:

[maths0]

Maintenant il faut que tu me rappelles pour et :
- la formule explicite en fonctions de n
- la nature
- lepremier terme.
- la raison.

[Xeniuss]

j'ai essayé pour la 4) mais sa laisse a désirer
wo= 3 x 2^1=6 w1= 3 x 2^2=12 w2= 3 x 2^3= 24


d'où (3x2^1)+(3x2^2)+(3x2^3)+...+(3x2^n)
S= 3((2^1)+(2^2)+(2^3)+..+(2^n))
S= ((1-2^n)/(1-2)) x 3


et la je sais plus quoi faire :/

[Xeniuss]

Maintenant il faut que tu me rappelles pour et :
- la formule explicite en fonctions de n
- la nature
- lepremier terme.
- la raison.

Est une suite géométrique de raison b=2 et de premier terme wo=3


Est une suite arithmétique de raison a=-4 et de premier terme to=3

[maths0]

Quelle est la formule qui donne la somme des termes d'une suite arithmétique ?
Quelle est la formule qui donne la somme des termes d'une suite géométrique ?

[Xeniuss]

Désolé mais mon ordi bug beaucoup c'est pour cela que je prend du temps pour répondre :/

[maths0]

Est une suite géométrique de raison b=2 et de premier terme wo=3


Est une suite arithmétique de raison a=-4 et de premier terme to=3

Attention lorsque l'on met entre parenthèse on parle de la suite, lorsqu'on enlève les parenthèses on parle des termes.
On écrire alors: :

[Xeniuss]

Quelle est la formule qui donne la somme des termes d'une suite arithmétique ?
Quelle est la formule qui donne la somme des termes d'une suite géométrique ?

La somme des termes d'une suite géométrique est donnée par la formule :

La somme des termes d'une suite arithmétique est donnée par la formule :

[Xeniuss]

Ha oui autant pour moi merci :)

[maths0]

Pour une suite arithmétique, pour faire la somme du premier au dernier:



Pour une suite géométrique, pour faire la somme du premier au dernier:

(avec q raison de la suite)



Maintenant on veut:
: Combien il y a de termes ?

[Xeniuss]

Pour une suite arithmétique, pour faire la somme du premier au dernier:



Pour une suite géométrique, pour faire la somme du premier au dernier:

(avec q raison de la suite)



Maintenant on veut:
: Combien il y a de termes ?

Il y a n termes

[maths0]

Raté ! c'est un gros piège et un gros problème des suites, et comprendre cela c'est faire un grand pas !
Si on somme les termes de la suite :
De 0 à 0:
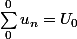
: 1 terme
De 0 à 1:
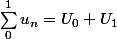
: 2 termes
De 0 à 2:
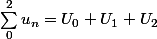
: 3 termes
De 0 à 3:
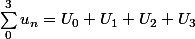
: 4 termes
De l à m:
: Combien de terme ?
De 0 à n:
: Combien de terme ?

[Xeniuss]

Raté ! c'est un gros piège et un gros problème des suites, et comprendre cela c'est faire un grand pas !
Si on somme les termes de la suite :
De 0 à 0:
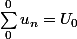
: 1 terme
De 0 à 1:
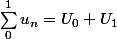
: 2 termes
De 0 à 2:
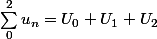
: 3 termes
De 0 à 3:
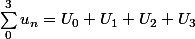
: 4 termes
De l à m:
: Combien de terme ?
De 0 à n:
: Combien de terme ?

Ha oui il y a n+1 termes de o à n non??

[maths0]

Oui et avec:
De l à m:
: Combien de termes ?
Car là tu es dans un exemple simple on pourrait te dire calculer la somme des termes pour n=5 à n=24 il y aurait combien de termes d'ailleurs ?

[Xeniuss]

de l à m il y à 2 termes
et de 5 à 24 il y a 20 termes