Problèmes d’algébre

[Tonio99]

Bonjour,
J’ai un DM de maths dans lequel je coince sur un exercice.
On me demande de déterminer un endormorphisme f de R3 qui vérifie Kerf = Vect((1,0,0),(1,1,1))
J’ai quelques idées comme quoi je vais me retrouver avec x et y car avec le vect c’est de dim2 (ce que je ne suis pas sur). Sinon aucune idée. Avez vous des idées pour me mettre sur la piste ?
Merci d’avance.

[Pseuda]

Bonjour,

Un endomorphisme est déterminé par l'image d'une base. Tu as déjà 2 vecteurs qui forment une famille libre, et qui ont pour image le vecteur nul.
Il suffit de choisir un 3ème vecteur (de ton choix) qui forme avec les 2 autres une famille libre, cela fera une base de R3, et de lui "inventer" une image.

[Ben314]

Salut,
Autre option (plus "terre à terre") : tu écrit que la matrice de ton endomorphisme, c'est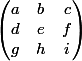 et tu regarde ce que ça donnent les équations et .

Et tu réfléchi aussi un peu au fait que tu veut que le noyau de ton application contienne (1,0,0) et (1,1,1) donc tout le s.e.v. engendré par ces deux vecteurs, mais tu veut aussi qu'il ne contienne rien de plus.
Est-ce que tu vois ce que ça signifie concernant la matrice ?

[Tonio99]

Re, alors je viens tout juste à peine de commencer les matrices en cours donc j’ai quelques bases, cependant je ne vois pas trop à quoi cela correspond.

[chan79]

On me demande de déterminer un endormorphisme f de R3 qui vérifie Kerf = Vect((1,0,0),(1,1,1))

On peut penser à la projection orthogonale sur la droite vectorielle dirigée par le vecteur , produit vectoriel de (1,0,0) et (1,1,1)

[Tonio99]

Bonjour,

Un endomorphisme est déterminé par l'image d'une base. Tu as déjà 2 vecteurs qui forment une famille libre, et qui ont pour image le vecteur nul.
Il suffit de choisir un 3ème vecteur (de ton choix) qui forme avec les 2 autres une famille libre, cela fera une base de R3, et de lui "inventer" une image.

Re Bonjour, alors j’ai pris comme vecteur, (1,0,1) J’ai une question est ce que j’ai vraiment le droit de prendre un vecteur quelconque pour résoudre l’exercice ? Ensuite pour trouver l’endomorphisme je dois bien égaliser f(e1) f(e2) et f(e3) au vecteur nul ? e1 e2 et e3 etant les trois vecteurs. Merci d’avance

[capitaine nuggets]

Salut!

Soit un endomorphisme d'espaces vectoriels.
Notons et ; puisque 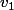et 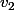sont non colinéaires on peut considérer leur produit vectoriel . Par construction, la famille 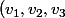est donc une base de : c'est-à-dire que pour tout , on peut trouver trois scalaires (uniques) tels que l'on ait . Or donc par définition toutes les combinaisons linéaires des vecteurs 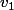et 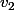sont envoyées sur par , c'est-à-dire que :



P.S. : Là j'ai pris le produit vectoriel de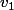 et 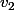pour compléter la famille libre de afin d'en faire une base parce qu'on est dans et qu'on peut avoir un point de vue géométrique, mais j'aurais pu prendre n'importe quel vecteur de , pourvu que cela forme une base de .

[Tonio99]

Ah merci pour ce renseignement, du coup je trouve le vecteur v3= (0,1,-1). Petite derniére question car j’ai encore un peu de mal à visualisé. Comment en déduire l’endomorphisme pour terminé cet exercice ? Une petite piste ?
Merci d’avance

[pascal16]

version rapide, sauf erreur de ma part :
Kerf = Vect((1,0,0),(1,1,1))
troisième vecteur : u = α (1,0,0) ⋀ (1,1,1)

on peut jouer avec α
α tel que ||u||=1, tu as un projection orthogonale de direction Vect((1,0,0),(1,1,1)) sur Vect(u)
sinon, tu as un projection orthogonale couplée à une homothétie de rapport ||u||.

autre choix de u : simplement dans le complémentaire de Vect((1,0,0),(1,1,1))
la projection n'es plus orthogonale et c'est moins facile à voir

[Pseuda]

Petite derniére question car j’ai encore un peu de mal à visualisé. Comment en déduire l’endomorphisme pour terminé cet exercice ? Une petite piste ?
Merci d’avance

Bonjour,

Tu peux prendre tout simplement l'endomorphisme qui à v1 et v2 associe le vecteur nul, et à v3 associe lui-même. Cela fera ainsi la projection orthogonale sur la droite vectorielle générée par v3.

u(v1)=0
u(v2)=0
u(v3)=v3

[Ben314]

Perso, il me semble quand même que c'est "à peine plus simple" (sic...) de partir de ça :
et
Qui nous dit immédiatement est sans calculs que les endomorphismes tels que 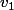et 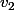soient dans , c'est très exactement ceux de la forme où sont des constantes.
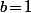La seule mini vague astuce, c'est de dire que, pour que le noyau de ne soit que et pas plus, ben ça veut dire précisément qu'il existe un vecteur tel que et donc ça signifie qu'il ne faut pas prendre tout les 3 nuls (donc vu qu'on demande juste un exemple, autant prendre et )

Mais, bon, c'est vrai, pourquoi faire simple et sans calculs quand on peut faire compliqué et avec calculs...

[Pseuda]

Il est demandé une solution, pas toutes les solutions, ce qui, parfois, peut paraître plus compliqué.

[Tonio99]

Merci donc au final si j’ai trouvé f(x,y,z)=(0,y,z) ou alors f(x,y,z)=(0,y,-y) ce qui revient au meme. Par contre je sais pas si ça colle avec la réponse de ben

[Ben314]

Merci donc au final si j’ai trouvé f(x,y,z)=(0,y,z) ou alors f(x,y,z)=(0,y,-y) ce qui revient au meme. Par contre je sais pas si ça colle avec la réponse de ben

Dans chacun des deux cas, ça vaut combien f(1,1,1) ?
Est-ce que "ça revient au même" ?
Est-ce que (1,1,1) est dans le noyau de f ?

[Tonio99]

C’est juste avec mon exemple que ça marche donc erreur de ma part. J’ai peut etre une idée avec (y-z,0,0). Je pense que je vais vite renoncé voyant que je tourne en rond depuis bien trop longtemps.... Mais merci quand même car cela m’as permis d’avancer un peu