Salut,
On te donne
 = 2x^2 - 4x + 1)
Ton objectif est en fait de savoir si on a effectivement la forme canonique de T(x) qui est
^2 - \frac{3}{2}))
ou bien si c'est faux.
Tu as deux possibilités: soit tu pars de l'expression
^2 - \frac{3}{2}))
et tu la développes. C'est la méthode pas raffinée qui ne te fera pas beaucoup travailler. La deuxième méthode plus instructive est de partir de
 = 2x^2 - 4x + 1)
et de la mettre sous forme canonique puis comparer avec celle qu'on te donne. Je vais te détailler les deux pour que tu comprennes... car tu devras en faire plusieurs en cours et aux examens.
Méthode 1: Développer
^2 - \frac{3}{2}))
Tout d'abord, tu sais que (a - b)^2 = a^2 - 2ab + b^2.
Cela veut dire que
^2 = x^2 - 2 \times x \times \sqrt{2} + (\sqrt{2})^2 = x^2 - 2 \sqrt{2} x + 2)
.
Donc en fait,
^2 - \frac{3}{2} = x^2 - 2 \sqrt{2} x + 2 - \frac{3}{2} = x^2 - 2 \sqrt{2}x + \frac{4}{2} - \frac{3}{2} = x^2 - 2\sqrt{2}x + \frac{1}{2})
.
En tout multipliant par 2:
^2 - \frac{3}{2} ) = 2(x^2 - 2 \sqrt{2}x + \frac{1}{2}) = 2x^2 - 4 \sqrt{2} x + 1)
On constate que cette écriture est différente de celle de T, ce qui veut dire que ce n'est pas la bonne forme canonique.
Méthode 2: On part de T(x) = 2x^2 - 4x + 1 et on cherche la forme canonique.
La première chose que l'on fait pour trouver la forme canonique, est de prendre le "a" (dans ax^2 + bx + c) en facteur. Ici a = 2.
 = 2(x^2 - 2x + \frac{1}{2}))
La deuxième chose que l'on fait est qu'on regarde les termes contenant x: x^2 - 2x qui est de la forme
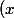^2 - 2 \times x \times 1)
. C'est le début de (a - b)^2 = a^2 - 2ab + b^2 avec a = x et b = 1. Mais on voit bien qu'il manque le +b^2 non? donc on l'ajoute et on le retranche pour conserver l'égalité. On ne touche pas le 1/2 pour le moment
 = 2(x^2 - 2x + 1 - 1 + \frac{1}{2}) = 2((x - 1)^2 - 1 + \frac{1}{2})
. C'est bon, on a formé le x^2 - 2x + 1= (x - 1)^2 !
On continue en regroupant -1 + 1/2 = -2/2 + 1/2 = -1/2
 = 2((x - 1)^2 - 1 + \frac{1}{2}) = 2((x - 1)^2 - \frac{1}{2}) = 2(x - 1)^2 - 1)
On voit bien que ce n'est pas la même chose que la formule donnée.
Maintenant il faut que essayes avec d'autres trinômes pour voir si tu arrives à trouver la forme canonique. N'applique pas des formules, suis la méthode expliquée...
