Dm prepa ECS Produit de nb complexes

[oceanevp]

ennoncé : Qn = le produit de sin kpi/2n pour k allant de 1 à n-1
= le produit de sin kpi/2n pour k allant de n+1 à 2n-1

Rn = le produit de sin kpi/2n pour k allant de 1 à 2n-1

Montrer que Rn = Qn ^2

Je suis bloquée à la question 2, svp si quelqu'un veut bien m'aider je me retrouve avec le produit des sin kpi/2n au carré pour k allant de n+1 à 2n-1

[Ben314]

Salut,
Ben, je sais pas si c'est "super niveau supérieur" de constater que, si A=B alors Ax1xB=A²...

[oceanevp]

Niveau superieur ou pas, je ne comprend pas en quoi A = B puisqu'ils n'ont pas les mêmes indices

[anthony_unac]

Bonsoir,
Si, Qn = le produit de sin kpi/2n pour k allant de 1 à n-1
= le produit de sin kpi/2n pour k allant de n+1 à 2n-1 alors que vaut le produit de sin kpi/2n pour k allant de 1 à n ?
De la même manière que vaut le produit de sin kpi/2n pour k allant de n à 2n-1 ?

[Razes]

Tu as juste à scinder 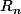en produit de deux termes en choisissant les bons indices.