Problème de proba en prépa ECS 2

[krokos55]

Bonjour j’aimerais bien un peu d’aide afin de résoudre le problème de maths suivant :

Une loterie a lieu toute les semaines, 100 billets sont en vente 10 sont gagnants
Je dispose de 7 euros
Vaut il mieux acheter tout les billets la même semaine ou acheter un billet par semaine ?



Merci beaucoup pour votre aide

[Joker62]

ça dépend du prix du billet on va dire.

[krokos55]

désolé le prix du billet vaut 1 euro
j'ai oublié de le préciser

[fahr451]

bonjour

revient à comparer une loi hypergéométrique à une géométrique

[krokos55]

merci bcp
en somme si j'achete tous les billets la meme semaine c'est une loi hypergeométrique
sinon c'est une loi géométrique
au final il faut comparer les esperances de chacune de ces lois avec
X la var égale au nombre de ticket achetés qui sont gagnant?
c'est ca ou pas ?

[fahr451]

pas les espérances mais la proba de gagner

proba de ne pas gagner au moins une fois
cas 1


7 parmi 90 / 7 parmi 100

cas 2

(90 /100)^7

[Isomorphisme]

Bonjour,

Contrairement à ce qu'a dit fahr451, je ne pense pas que le 2ème cas soit une géométrique (qui suppose qu'on dispose d'une somme infinie en théorie) mais bien une binômiale.

Par ailleurs, il faut comparer les espérances de gain et non les probabilités de gain (le joueur peut gagner potentiellement 7 fois !!)

Le premier cas peut être modélisé par une loi hypergéométrique
où , et
et dont l'espérance est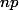

Le deuxième cas peut être modélisé par une loi binômiale dont l'espérance est la même que celle d'une hypergéo i.e.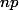

Donc en espérance, ces deux stratégies sont les mêmes. Toutefois, le risque n'est pas le même, puisque la variance est dans le premier cas égale à inférieure à (variance de la 2ème stratégie).

Par conséquent, la 1ère stratégie est la meilleure en termes de risque.

[fahr451]

contrairement à ce qu 'a écrit isomorphisme je pense que la question (pas clirement posée) est de savoir si on gagne ou pas

ds le deuxième cas le nbre de billets gagnants est bien une binômiale

mais le fait de ne pas gagner est un processus géométrique

(nbre d 'échecs avant le premier succès)

on ne demande pas combien on va gagner mais si on gagne

pas si clair en fait

[Isomorphisme]

Encore une fois, même si la question n'est pas explicite, il est clair que si on investit 7 € (autrement dit on achète 7 billets potentiellement gagants), on s'intéresse plus au gain moyen qu'à la probabilité de gagner au moins une fois (dans l'hypothèse où le gain associé à chaque billet est le même). En effet, je ne veux pas gagner au moins une fois, mais avoir le rendement maximal sur mes 7 € investis, c'est du bon sens (financier !!) !
Je persiste et signe donc :happy2:

P.S. : la phrase "le fait de ne pas gagner est un processus géométrique" n'a pas de sens. En revanche, le fait de gagner ou pas peut être modélisé par un schéma bernoullien.
En outre, c'est le nombre de billets nécessaires pour gagner une fois qui est régi par une loi géométrique (mais comme je l'ai déjà dit, cela suppose qu'on dispose d'un capital infini en théorie, or je n'ai que 7€ ...)

[fahr451]

s il me suffit de gagner une seule fois pour toucher le gros lot (et vivre heureux le restant de mes jours) je préférerais la stratégie qui me donnera la meilleure proba de gagner une fois même si l'espérance de gain est plus faible
schéma bernoullien et non processus géométrique (même si tout le monde comprend sauf les puristes) je te l 'accorde

[Isomorphisme]

Oui mais dans ce cas-là il ne faut pas miser 7 € mais un seul € ! Dans l'énoncé, on peut supposer que le gain associé à chaque billet est le même. Il ne s'agit pas de gagner "le gros lot" mais de gagner le plus de fois (dans la limite de 7 fois) !

[fahr451]

on pourrait convenir que la question n 'est pas explicite il me semble