Implication
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
anassmsdq
- Membre Naturel
- Messages: 14
- Enregistré le: 11 Sep 2016, 14:07
-
 par anassmsdq » 25 Sep 2016, 20:19
par anassmsdq » 25 Sep 2016, 20:19
Bonsoir tout le monde .
je veux montrer que : quelque soit (x,y)

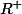
x+y=2


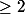
merci d'avance
-
bolza
- Membre Relatif
- Messages: 449
- Enregistré le: 04 Juin 2015, 10:15
-
 par bolza » 25 Sep 2016, 21:56
par bolza » 25 Sep 2016, 21:56
Bonsoir,
le moyen le plus simple que j'ai trouvé c'est que si x+y=2 alors cela signifie qu'il existe

avec

tel que

et

(où l'inverse mais ça ne change pas grand chose).
et donc le tout serait de voir si
^4+(1-\varepsilon)^4\ge 2)
....

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 25 Sep 2016, 22:04
par Lostounet » 25 Sep 2016, 22:04
anassmsdq a écrit:Bonsoir tout le monde .
je veux montrer que : quelque soit (x,y)

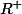
x+y=2


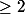
merci d'avance
Si x+y = 2 alors:
y^4 + x^4
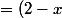^4 + x^4)


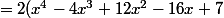 + 2)
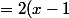^2(x^2 - 2x + 7) + 2)
>= 2
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
anassmsdq
- Membre Naturel
- Messages: 14
- Enregistré le: 11 Sep 2016, 14:07
-
 par anassmsdq » 25 Sep 2016, 22:30
par anassmsdq » 25 Sep 2016, 22:30
merci beacoup

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 26 Sep 2016, 08:52
par Lostounet » 26 Sep 2016, 08:52
Le cas d'égalité apparait alors pour x=y=1 avec cette forme canonique
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités

x+y=2
