Trigonométrie 1er S
26 messages
- Page 1 sur 2 - 1, 2
Trigonométrie 1er S
Bonjour, voila je suis bloqué a la question 2)a) de mon exercice , j'aimerai de l'aide
L'énoncé est en lien http://www.maths-forum.com/download/file.php?id=229
Merci d'avance
L'énoncé est en lien http://www.maths-forum.com/download/file.php?id=229
Merci d'avance
Re: Trigonométrie 1er S
Bonjour teambs,
Pour la question 2a, ta tension est maximum lorsque ton cosinus est égale à 1.
Pour la question 2b, il faut que tu détermine la valeur de ta variable t sachant que cos(2pi)=1. (modulo 2pi)
Pour la question 3, il faut que tu pose u(t)=220 et déterminer la valeur de t dans ton cosinus.
Pour la question 2a, ta tension est maximum lorsque ton cosinus est égale à 1.
Pour la question 2b, il faut que tu détermine la valeur de ta variable t sachant que cos(2pi)=1. (modulo 2pi)
Pour la question 3, il faut que tu pose u(t)=220 et déterminer la valeur de t dans ton cosinus.
Re: Trigonométrie 1er S
ludo54 a écrit:Bonjour teambs,
Pour la question 2a, ta tension est maximum lorsque ton cosinus est égale à 1.
Pour la question 2b, il faut que tu détermine la valeur de ta variable t sachant que cos(2pi)=1. (modulo 2pi)
Pour la question 3, il faut que tu pose u(t)=220 et déterminer la valeur de t dans ton cosinus.
Pour la 2b) j'ai fais :
Cos(100π * t*π/4 ) = 2π
Cos(100π * t) = 2π - π/4
Cos(100π * t) = 8π/4 - π/4
Cos(100π * t) = 7π/4 [2π]
Re: Trigonométrie 1er S
Et je sais pas si c'est une bonne idée de continuer en faisant :
Cos(100π * t) = 7π/4 [2π]
Cos(t) = 7π/4*100π
Cos(t) = 7/400
Cos(t) = 0,0175
Cos(100π * t) = 7π/4 [2π]
Cos(t) = 7π/4*100π
Cos(t) = 7/400
Cos(t) = 0,0175
Re: Trigonométrie 1er S
Non, il me semble pas que ce soit une bonne idée d'écrire qu'un cosinus est (environ) égal à 6.28 : il me semble bien que c'est toujours compris entre -1 et 1 un cosinus, non ?teambs a écrit:ludo54 a écrit:Cos(100π * t*π/4 ) = 2π
Sans parler du fait qu'il me semble bien que la valeur d'un truc du style Cos(100π * t*π/4 ), ça devrait tout de même un peu dépendre de la valeur de t (donc ne pas être égal à 2π quelque soit t) non ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Trigonométrie 1er S
Ben314 a écrit:Non, il me semble pas que ce soit une bonne idée d'écrire qu'un cosinus est (environ) égal à 6.28 : il me semble bien que c'est toujours compris entre -1 et 1 un cosinus, non ?teambs a écrit:ludo54 a écrit:Cos(100π * t*π/4 ) = 2π
Sans parler du fait qu'il me semble bien que la valeur d'un truc du style Cos(100π * t*π/4 ), ça devrait tout de même un peu dépendre de la valeur de t (donc ne pas être égal à 2π quelque soit t) non ?
Donc je devrai plutôt écrire Cos(100π * t*π/4 ) = 1 non ?
Re: Trigonométrie 1er S
ludo54 a écrit:Oui il faut que tu écrive Cos(100pi*t+(pi/4))=1
Cos(100π * t + π/4 ) = 1
Cos(100π * t + π/4 ) = 1 - cos( π/4 )
Cos(100π * t ) =
Cos( t ) =
Cos( t ) =
Cos( t ) =
Re: Trigonométrie 1er S
Je te conseillerais plutôt d'utiliser la seconde relation que je t'ai donné.
soit : 100pi*t+(pi/4)=2pi
j'ai trouvé t = (7/400)=0.0175 seconde.
soit : 100pi*t+(pi/4)=2pi
j'ai trouvé t = (7/400)=0.0175 seconde.
Re: Trigonométrie 1er S
C'est ce que j'avais fais précédemment :
Cos(100π * t*π/4 ) = 2π
Cos(100π * t) = 2π - π/4
Cos(100π * t) = 8π/4 - π/4
Cos(100π * t) = 7π/4
Cos(t) = 7π/4*100π
Cos(t) = 7/400
Cos(t) = 0,0175
Cos(100π * t*π/4 ) = 2π
Cos(100π * t) = 2π - π/4
Cos(100π * t) = 8π/4 - π/4
Cos(100π * t) = 7π/4
Cos(t) = 7π/4*100π
Cos(t) = 7/400
Cos(t) = 0,0175
Re: Trigonométrie 1er S
non tu n'as pas le droit de dire que Cos(100π * t+π/4 ) = 2π!
Cos(100π * t+π/4 )=1
et on sait que :
cos(2π)=1 soit 100π * t+π/4=2π.
Tu comprends?
donc t=0.0175s et non cos(t)=0.0175s.
Cos(100π * t+π/4 )=1
et on sait que :
cos(2π)=1 soit 100π * t+π/4=2π.
Tu comprends?
donc t=0.0175s et non cos(t)=0.0175s.
Re: Trigonométrie 1er S
Ah d'accord , donc a gauche je dois retire le cos et laisser comme ca ?
100π * t*π/4 = 2π
100π * t = 2π - π/4
100π * t = 8π/4 - π/4
100π * t = 7π/4
t= 7π/4*100π
t = 7/400
t = 0,0175
100π * t*π/4 = 2π
100π * t = 2π - π/4
100π * t = 8π/4 - π/4
100π * t = 7π/4
t= 7π/4*100π
t = 7/400
t = 0,0175
Re: Trigonométrie 1er S
ludo54 a écrit:oui donc lorsque t = 0.0175 s, u(t) = Umax.
D'accord merci beaucoup et pour la question 3) je dois donc remplacer t par sa valeur ?
u(t) = 220
u(t) = 220
Re: Trigonométrie 1er S
il faut que tu trouve la valeur de t pour l'équation :
220 = 220 * racine(2 )* cos (100π * t+π/4 )
Détermine la valeur du cosinus pour laquelle tu as u(t)=220 et à partir de la tu peux déterminer la valeur de t.
220 = 220 * racine(2 )* cos (100π * t+π/4 )
Détermine la valeur du cosinus pour laquelle tu as u(t)=220 et à partir de la tu peux déterminer la valeur de t.
Re: Trigonométrie 1er S
J'ai trouver :
220 * * cos(100π * t+π/4 ) = 220
* cos(100π * t+π/4 ) = 220
 * cos(100π * t+π/4 ) = 220/220
* cos(100π * t+π/4 ) = 220/220
 * cos(100π * t+π/4 ) = 1
* cos(100π * t+π/4 ) = 1
cos(100π * t+π/4 ) = 1/
t = 1/ - cos(100π ) - cos (π/4 )
- cos(100π ) - cos (π/4 )
t = 1/ - 1 -
- 1 - 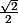
t = -1
220 *
cos(100π * t+π/4 ) = 1/
t = 1/
t = 1/
t = -1
Re: Trigonométrie 1er S
il y à plusieurs valeurs de t, cette équation est vérifiée pour tout nombre entier.
26 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 79 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
