Trigonométrie 1er s

[Ily007]

Bonjour, je suis en première et j’ai un peu de mal avec ce devoir maison. Alors j’aimerais avoir un peu d’aide. Merci d’avance
Le sujet est le suivant :

Soit (O ; I ; J) un repère orthonormé direct. A est le point de coordonnées (4 ; 0) et B est le point tel que le triangle OAB est isocèle en O avec
( vecteurOA ; vecteurOB ) = pi/6 .
K est le milieu de [AB].
1a) Déterminer les coordonnées du point B puis celles du point K.
1b) Exprimer les coordonnées de K en fonction de cos pi/12 et sin pi/12 .
2) A l'aide de la question 1 et de l'écran de calcul formel ci-dessous, donner les valeurs exactes de cos pi/ 12 et sin pi/ 12 : (les V représentent des racines carrées)
1/sqrt(8+4*sqrt(3))
--> 1/4 (-V2 + V6)
(2+sqrt(3))/sqrt(8+4*sqrt(3))
--> 1/4 (V2 + V6)

Donc pour la 1a) je me suis dit que puisque le point B correspond à un angle de pi/6 ses coordonnées pourrais être B(1/2;sqrt(3)/2) en rapport avec le sinus et le cosinus mais je ne suis pas sûr.

[mathelot]

B a pour coordonnées polaires
calcule ses coordonnées cartésiennes

[Ily007]

Mais comment je fait , je doit le lire graphiquement ou le trouver par le calcul ?

[mathelot]

trouve les coordonnées de B grâce à des calculs:

on a le sens


et le sens (dans le demi plan d'équation x>0)

[Ily007]

Si j’utilise le cosinus et le sinus de pi/6 ça ne marche pas ?

[mathelot]

Si j’utilise le cosinus et le sinus de pi/6 ça ne marche pas ?

si ça marche, ça va te donner les valeurs numériques qui sont les fondements du calcul

[Ily007]

Ok alors je remplace x par sqrt(3)/2 et y par 1/2
r = sqrt((sqrt(3)/2)^2)+(1/2)^2)
(Thêta) =arctan((sin pi/6 )/(cos pi/6))
Mais je ne comprend pas à quoi correspond « r » et « thêta »

[mathelot]

les coordonnées de B



PS: r=4 et théta=pi/6

[Ily007]

Ah oui je vois et après je fais pareil avec k

[mathelot]

Ah oui je vois et après je fais pareil avec k

non, K est le milieu de [AB]. calcule ses coordonnées.

[Ily007]

donc pour k je trouve
((xa+xb)/2;(ya+yb)/2)
K((4+2sqrt(3)/2;(0+2)/2)
K(2+sqrt(3);1)

[Ily007]

Et ensuite pour la 2) j’ai calculé La longueur OK , avec
sqrt((xb-xa)^2+(yb-ya)^2)
Et je trouve
sqrt(8+4sqrt(3))
Mais après je ne sais pas comment faire pour trouver le cos et le sin de pi/12

[mathelot]

le point K a aussi comme coordonnées


on connait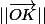 , on peut égaliser ses deux couples de coordonnées

[aymanemaysae]

Bonsoir ;

Puisque tu as presque fait l'exercice en calculant OK et les coordonnées du point K ;
je te propose l'approche suivante : (à propos , je viens de voir la proposition de mathelot , je pense que tu devrais continuer le chemin que tu as entrepris avec lui , et laisser mon approche à la fin pour vérifier les résultats que tu trouveras .)

[Ily007]

Mais si je doit exprimer les coordonnées en fonction de cos pi/12 et sin pi/12 est ce que je dois calculer la valeur exacte ?
( ps : merci beaucoup pour vos aides )

[mathelot]

Et ensuite pour la 2) j’ai calculé La longueur OK , avec
sqrt((xb-xa)^2+(yb-ya)^2)
Et je trouve
sqrt(8+4sqrt(3))
Mais après je ne sais pas comment faire pour trouver le cos et le sin de pi/12

simplifie , le radicande est un carré parfait

[Ily007]

D’accord, et est ce que j’en suis censé retomber sur les valeurs qu’on donne dans l’a question 2)
à savoir 1/sqrt(8+4(sqrt(3)) pour le cosinus et (2+sqrt(3))/sqrt(8+4sqrt(3)) pour le sinus ?

[mathelot]

les valeurs finales sont et son conjugué

[Ily007]

D’accords mais si je trouve ça a quoi me servent les chiffres que l´on me donne dans l’enoncé ( questions 2)?

[mathelot]

D’accords mais si je trouve ça a quoi me servent les chiffres que l´on me donne dans l’enoncé ( questions 2)?

c'est une étape intermédiaire dans les calculs