Demande de l'aide
24 messages
- Page 1 sur 2 - 1, 2
 Demande de l'aide
Demande de l'aide
Bonjour à tous ;
J'ai besoin de votre aimable aide pour pouvoir ensuite écrire un programme informatique.
Question : Comment peut-on trouver le rest de la devisions euclidienne a^n /p (où a,p et n sont des entiers) SANS calculer a^n?
Exemple : quel est le rest de cette division : 2^15/100
J'ai besoin de votre aimable aide pour pouvoir ensuite écrire un programme informatique.
Question : Comment peut-on trouver le rest de la devisions euclidienne a^n /p (où a,p et n sont des entiers) SANS calculer a^n?
Exemple : quel est le rest de cette division : 2^15/100
Re: Demande de l'aide
Aloha,
Si , alors
, alors 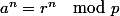 .
.
Tu as donc juste à calculer le reste de a par p, puis de l'élever à la puissance n.
Si
Tu as donc juste à calculer le reste de a par p, puis de l'élever à la puissance n.
« Je ne suis pas un numéro, je suis un homme libre ! »
Re: Demande de l'aide
Merci beaucoup ,c'est très gentil.
Est-que tu peux d
me donner la réponse de ces 3 exemple (désolée .c'est pour mieux comprendre )
.c'est pour mieux comprendre )
2^15/100
5^15/3
6^80/52
Est-que tu peux d
me donner la réponse de ces 3 exemple (désolée
 .c'est pour mieux comprendre )
.c'est pour mieux comprendre )2^15/100
5^15/3
6^80/52
Re: Demande de l'aide
Pour n un nombre entier premier et p = n , vous pouvez utiliser "Le Petit Théorème de Fermat" qui s'énonce comme suit: « si n est un nombre premier et si a est un entier non divisible par n, alors  est un multiple de n. ». Autrement dit, sous les mêmes conditions sur a et n :
est un multiple de n. ». Autrement dit, sous les mêmes conditions sur a et n :  .
.
Un énoncé équivalent est : « si n est un nombre premier et si a est un entier quelconque, alors est un multiple de n. »
est un multiple de n. »
Quant à votre exemple, nous avons \pmod {100})

 .
.
Un énoncé équivalent est : « si n est un nombre premier et si a est un entier quelconque, alors
Quant à votre exemple, nous avons
Modifié en dernier par aymanemaysae le 19 Fév 2016, 13:13, modifié 1 fois.
Re: Demande de l'aide
salut
une remarque : comme les puissances "explosent" très vite il est préférable de calculer par récurrence
en considérant la suite définie par récurrence ::


une remarque : comme les puissances "explosent" très vite il est préférable de calculer par récurrence
en considérant la suite définie par récurrence ::
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Demande de l'aide
Salut,
Dés que n est "un peu grand", il vaut nettement mieux ne pas utiliser la définition récursive des puissances (i.e. ) mais plutôt un truc proche de la dichotomie, à savoir
) mais plutôt un truc proche de la dichotomie, à savoir  et
et  qui permet de calculer
qui permet de calculer  avec une complexité de
avec une complexité de )) plutôt que
plutôt que ) .
.
C'est par exemple comme ça qu'on implémente la méthode RSA qui demande de calculer de nombreuse très très grandes puissances d'entiers.
Dés que n est "un peu grand", il vaut nettement mieux ne pas utiliser la définition récursive des puissances (i.e.
C'est par exemple comme ça qu'on implémente la méthode RSA qui demande de calculer de nombreuse très très grandes puissances d'entiers.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Demande de l'aide
Ben314 a écrit:Salut,
Dés que n est "un peu grand", il vaut nettement mieux ne pas utiliser la définition récursive des puissances (i.e.) mais plutôt un truc proche de la dichotomie, à savoir
et
qui permet de calculer
avec une complexité de
plutôt que
.
C'est par exemple comme ça qu'on implémente la méthode RSA qui demande de calculer de nombreuse très très grandes puissances d'entiers.
certes oui pour optimiser le temps de calcul ....sur des grosses machines ....
moi je parlais essentiellement sur des machines type celles qu'on a au lycée ou tableur .... pour lesquelles les entiers ne sont pas "très grands" .... "trop grands"
avec un programme ou un travail sur tableur pour des puissances raisonnables (de l'ordre du millier) ma méthode suffit amplement ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Demande de l'aide
Merci à tous 
Grace à votre aide j'ai trouver ma réponse



Quel hasard ! C'est exactement ce que je voulais écrire comme programme
Grace à votre aide j'ai trouver ma réponse
Quel hasard ! C'est exactement ce que je voulais écrire comme programme

Re: Demande de l'aide
zygomatique a écrit:certes oui pour optimiser le temps de calcul ....sur des grosses machines ....
Je sais pas ce que c'est que tu appelle "une grosse machine", mais à l'heure actuelle, tout ce qui permet d'accéder à internet (y compris le plus petit smart-phone qui soit) utilise RSA pour la sécurité et donc calcule en pagaille des trucs du style a^n mod p où a,p et n sont de l'ordre de 10^300.
Et si tu essaye d'utiliser un algo. en O(n) pour un n de l'ordre de 10^300, tu est pas près d'avoir la réponse.
Après, ce que je raconte, ça risque d'être "pour du beurre" si le contexte de l'exo. c'est uniquement du "niveau zéro" de programmation.
Mais assez souvent, lorsque l'on demande à des étudiants de programmer des puissances modulaires, le but, ensuite, c'est de programmer RSA et là, c'est quand même pas con que tu puisse tester ton algo avec de "vraies" clefs RSA et pas uniquement avec des nombre tout petits.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Demande de l'aide
je suis bien d'accord avec toi .... mais au niveau lycée comme je l'ai dit (et même si on voit un peu les codes RSA tout en restant sur la théorie) il est très rare (pour ne pas dire jamais) qu'on travaille numériquement avec des nombres de cette taille ...
bien sur on résout par exemple ce genre d'exo : déterminer a^b [n] (avec b = 2016 au hasard)
et on commence à le faire avec "un tableau de congruence" (surtout quand on ne connaît pas Fermat) puis on utilise ensuite les propriétés des congruences .... pour conclure ....
ou alors on le fait avec un tableur ou un programme comme je l'ai dit et c'est bien suffisant ....
quand les machines avec lesquelles on travaille ne peuvent contenir des entiers avec plus de 12 ~ 15 chiffres ....
au lycée en spé math (mais même en général) on fait beaucoup de culturel :: numéro Sécu, n°, ISBN, code BIC ou IBAN, chiffrement affine, de Hill, .... pour découvrir et manipuler de façon élémentaire les objets mathématiques ... mais il ne faut pas trop forcer ....
bien sur on résout par exemple ce genre d'exo : déterminer a^b [n] (avec b = 2016 au hasard)
et on commence à le faire avec "un tableau de congruence" (surtout quand on ne connaît pas Fermat) puis on utilise ensuite les propriétés des congruences .... pour conclure ....
ou alors on le fait avec un tableur ou un programme comme je l'ai dit et c'est bien suffisant ....
quand les machines avec lesquelles on travaille ne peuvent contenir des entiers avec plus de 12 ~ 15 chiffres ....
au lycée en spé math (mais même en général) on fait beaucoup de culturel :: numéro Sécu, n°, ISBN, code BIC ou IBAN, chiffrement affine, de Hill, .... pour découvrir et manipuler de façon élémentaire les objets mathématiques ... mais il ne faut pas trop forcer ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Demande de l'aide
Certes, certes, sauf que là il me semble bien qu'on est dans le forum supérieur et pas dans le forum Lycée et, dans le supérieur, de plus en plus souvent, on apprend l'algo. avec des langages du type Python (c.f. message de Chang çi dessus) qui n'ont pas de limite prédéterminées sur les entiers et qui permettent donc de tester RSA en "vrai grandeur" sans que ça demande aucun travail supplémentaire.
A condition, évidement... d'avoir tapé un algo. de puissance modulaire en O(ln(n)) et pas en O(n)...
A condition, évidement... d'avoir tapé un algo. de puissance modulaire en O(ln(n)) et pas en O(n)...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Demande de l'aide
certes, certes, certes .... il est évident que Reihan s'est posé la question d'un algorithme en O(ln(n)) plutôt qu'en O(n) pour résoudre son pb ....
quand on débute, on débute .... après on peut se (le professeur peut) poser la question de l'optimisation .... pour les grands nombres ....
chan79 a fait exactement ce que j'ai dit ...
et j'apprécie tout à fait l'intervention pertinente de Robot pour dire que pour des grands nombres on peut améliorer le processus ...
mais je pense que (que ce soit au lycée ou même en début de supérieur) faire seul ce qu'a fait chan79 est déjà un bon début ...

quand on débute, on débute .... après on peut se (le professeur peut) poser la question de l'optimisation .... pour les grands nombres ....
chan79 a fait exactement ce que j'ai dit ...
et j'apprécie tout à fait l'intervention pertinente de Robot pour dire que pour des grands nombres on peut améliorer le processus ...
mais je pense que (que ce soit au lycée ou même en début de supérieur) faire seul ce qu'a fait chan79 est déjà un bon début ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Demande de l'aide
Tu pense... ce que tu veut...
Perso., quand j'enseigne l'algo. (donc par exemple cette année...) c'est justement cet exemple là que je prend pour montrer qu'il y a plusieurs algo. aussi simples les uns que les autres (*) qui conduisent à des résultats aussi différents (en terme de complexité)
(*) Je pense pas que soit une formule "hors de porté" d'un étudiant...
soit une formule "hors de porté" d'un étudiant...
Aprés, on peut effectivement faire très exactement ce qui se fait au lycée : mettre des titres ronflants style "cours d'algorithmique" en évitant surtout de parler de quoi que ce soit qui puisse ressembler à de l'algorithmique, même (voire surtout...) lorsque l'occasion se présente facilement...
Perso., quand j'enseigne l'algo. (donc par exemple cette année...) c'est justement cet exemple là que je prend pour montrer qu'il y a plusieurs algo. aussi simples les uns que les autres (*) qui conduisent à des résultats aussi différents (en terme de complexité)
(*) Je pense pas que
Aprés, on peut effectivement faire très exactement ce qui se fait au lycée : mettre des titres ronflants style "cours d'algorithmique" en évitant surtout de parler de quoi que ce soit qui puisse ressembler à de l'algorithmique, même (voire surtout...) lorsque l'occasion se présente facilement...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Demande de l'aide
je suis bien d'accord ...
je veux simplement dire que dans un premier temps ce n'est pas la complexité d'un algorithme qui interpelle un élève/étudiant ... mais le fait de faire un programme qui tourne et réponde à la question ....
et je suis curieux de savoir quel pourcentage d'étudiants vont utiliser spontanément ton procédé (bien plus efficace évidemment)
(*) : malheureusement je vois bon nombre d'élèves de TS avoir beaucoup de mal avec les exposants ....
je veux simplement dire que dans un premier temps ce n'est pas la complexité d'un algorithme qui interpelle un élève/étudiant ... mais le fait de faire un programme qui tourne et réponde à la question ....
et je suis curieux de savoir quel pourcentage d'étudiants vont utiliser spontanément ton procédé (bien plus efficace évidemment)
(*) : malheureusement je vois bon nombre d'élèves de TS avoir beaucoup de mal avec les exposants ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Demande de l'aide
Réponse facile : jusque là, ça ne m'est jamais arrivé.zygomatique a écrit:et je suis curieux de savoir quel pourcentage d'étudiants vont utiliser spontanément ton procédé (bien plus efficace évidemment)
A chaque fois, une fois qu'on a écrit une première procédure en O(n), je leur demande comment ils procèderais si a la main (i.e. sans calculette) on leur demandait de calculer 2^256 en leur donnant comme (grosse) indication que : si,si, c'est faisable, mais il faut un peu réfléchir (et pas se gourer, évidement).
Avec le 256 qui est une puissance de deux, il arrive (mais pas toujours...) que certains aient l'idée de "casser" la puissance en la divisant 2 (plus précisément de faire uniquement des élévations au carré successives)
Et s'ils n'ont pas l'idée, je leur la donne (dans le cas de 256) et je leur demande ensuite si il voient comment faire dans un cas plus général (i.e. un exposant non puissance de 2).
De même, des fois, il y en a qui trouvent, des fois non (au pif je dirait 50/50...)
Ensuite, on écrit l'algo. correspondant et on compare sa complexité avec celle du premier algo.
C'est souvent le premier algo. où je fait un calcul de complexité vu qu'a mon avis, ça montre bien la pertinence de la notion de "calcul de complexité" sur un cas très simple.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Demande de l'aide
merci beaucoup pour ces précisions ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Demande de l'aide
Reihan a écrit:Merci à tous
Grace à votre aide j'ai trouver ma réponse



Quel hasard ! C'est exactement ce que je voulais écrire comme programme
juste une remarque
Si tu veux par exemple
Mais on peut montrer (par récurrence par exemple) que
Si n est très grand, on peut étudier la suite (périodique) des
On doit pouvoir inclure cette étude dans le programme.
Par exemple
Quelle est la valeur de
Re: Demande de l'aide
M. Chan79, par votre méthode j'ai trouvé que pour  on a :
on a :






et comme 201620162016 est un multiple de 6, donc .
.
Merci.
et comme 201620162016 est un multiple de 6, donc
Merci.
Re: Demande de l'aide
aymanemaysae a écrit:.
Bien vu, j'ai la même chose.
Dans le même genre:
A quoi est congru
Modifié en dernier par chan79 le 22 Fév 2016, 14:57, modifié 1 fois.
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 20 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :

