Résoudre z^3=2
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
phi27
- Messages: 3
- Enregistré le: 30 Déc 2015, 14:49
-
 par phi27 » 30 Déc 2015, 14:52
par phi27 » 30 Déc 2015, 14:52
Bonjour
Comment résoudre
résoudre z^3=2 ?
Merci
-
Robot
 par Robot » 30 Déc 2015, 14:55
par Robot » 30 Déc 2015, 14:55
Ensuivant les indications
données ici.
-
phi27
- Messages: 3
- Enregistré le: 30 Déc 2015, 14:49
-
 par phi27 » 30 Déc 2015, 14:58
par phi27 » 30 Déc 2015, 14:58
Merci
z² = r²e(2ithéta)
et z^3=r^3e(3ithéta)
on à 2=r^3e(3ithéta)
Comment mettre 2 sous forme e(ithéta) ?
-
Robot
 par Robot » 30 Déc 2015, 15:02
par Robot » 30 Déc 2015, 15:02
Revois ton cours sur le module et l'argument d'un nombre complexe, et le rapport avec la forme trigonométrique !
-
mathelot
 par mathelot » 30 Déc 2015, 17:59
par mathelot » 30 Déc 2015, 17:59
phi27 a écrit:Bonjour
Comment résoudre
résoudre z^3=2 ?
Merci
on a:
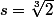
est solution (réelle) de l'équation.
en quotientant
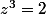
par
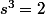
on trouve
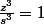
^3=1)
en posant
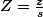

les solutions de cette dernière équation d'inconnue Z sont les racines cubique de l'unité soit

donc z=s ou
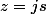
ou
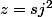
j étant égal à
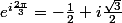

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 30 Déc 2015, 18:47
par zygomatique » 30 Déc 2015, 18:47
salut
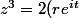^3 = 2e^{0i + ki2\pi})
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
phi27
- Messages: 3
- Enregistré le: 30 Déc 2015, 14:49
-
 par phi27 » 30 Déc 2015, 20:24
par phi27 » 30 Déc 2015, 20:24
zygomatique a écrit:salut
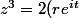^3 = 2e^{0i + ki2\pi})
....
Merci beaucoup
-
MouLou
- Membre Rationnel
- Messages: 578
- Enregistré le: 17 Sep 2015, 10:00
-
 par MouLou » 30 Déc 2015, 21:07
par MouLou » 30 Déc 2015, 21:07
Et Mathelot lui il a pas le droit à un petit merci? rooooo
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
