Variation équation

par **numero1** » 28 Nov 2015, 10:00

Bonjour, il y a une question à laquelle je n'arrive pas à répondre, svp :

On considère tous les triangles ABC rectangles en A vérifiant AB+AC=8cm.

La question c'est :
A l'aide du tableau de variation, expliquer pourquoi l'équation p(x)=16 admet 2 solutions. Déterminer ensuite par le calcul la valeur exacte de ces 2 solutions.

Je vous explique :
On a x la longueur d'un des côtés de l'angle droit. J'ai du déterminer l'intervalle auquel appartient x.
J'ai mis I= crochet vers la gauche 0 ; 8 crochet vers la droite

Puis exprimer le périmètre d'ABC en fonction de x
p(x)=8+ Racine (2x²-16x+64)

Etudier le sens de variation de P
x 0 4 8

p(x) flèche vers le bas 32 flèche vers le haut

Puis ensuite on arrive à cette question, que je n'arrive pas à faire svp

par **Carpate** » 28 Nov 2015, 11:43

numero1 a écrit:Bonjour, il y a une question à laquelle je n'arrive pas à répondre, svp :
On considère tous les triangles ABC rectangles en A vérifiant AB+AC=8cm.
La question c'est :
A l'aide du tableau de variation, expliquer pourquoi l'équation p(x)=16 admet 2 solutions. Déterminer ensuite par le calcul la valeur exacte de ces 2 solutions.
Je vous explique :
On a x la longueur d'un des côtés de l'angle droit. J'ai du déterminer l'intervalle auquel appartient x.
J'ai mis I= crochet vers la gauche 0 ; 8 crochet vers la droite
Puis exprimer le périmètre d'ABC en fonction de x
p(x)=8+ Racine (2x²-16x+64)
Etudier le sens de variation de P
x 0 4 8
p(x) flèche vers le bas 32 flèche vers le haut
Puis ensuite on arrive à cette question, que je n'arrive pas à faire svp

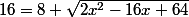
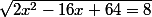
Tu obtiendras une équation équivalente en élevant les 2 termes au carré (car ils sont positifs)
Et ça se simplifie ...

par **numero1** » 28 Nov 2015, 11:55

Carpate a écrit: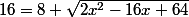

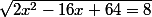
Tu obtiendras une équation équivalente en élevant les 2 termes au carré (car ils sont positifs)
Et ça se simplifie ...

Donc les 2 solutions c'est Racine (2x²-16+64) et 8+Racine (2x²-16x+64)

?
Vous avez été un peu vite, donc je suis pas sure que j'ai bon ^^

par **Carpate** » 28 Nov 2015, 12:03

numero1 a écrit:Donc les 2 solutions c'est Racine (2x²-16+64) et 8+Racine (2x²-16x+64)

?
Vous avez été un peu vite, donc je suis pas sure que j'ai bon ^^

Tu as mal lu ce que j'ai écrit :
Il faut élever au carré :

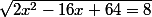
pour ne plus avoir de radical
Si tu as :

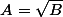
en élevant au carré tu obtiens :

par **numero1** » 28 Nov 2015, 12:07

Carpate a écrit:Tu as mal lu ce que j'ai écrit :
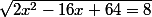
Il faut élever au carré : pour ne plus avoir de radical
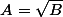
Si tu as : en élevant au carré tu obtiens :

Donc
Racine (2x²-16+64=8) en élevant au carré, la racine carré disparait et on a un carré donc on a
(2x²-16x+64=8)²
?

par **lop** » 28 Nov 2015, 12:10

En élevant au carré tu as :
2x^2-16x+64-8=0
Tu enlèves juste la racine
Mais est ce que 8 est bien en racine ou cest une faute de frappe ? Sinon ça fait 2x^2-16x=0

par **numero1** » 28 Nov 2015, 12:12

lop a écrit:En élevant au carré tu as :
2x^2-16x+64-8=0
Tu enlèves juste la racine
Mais est ce que 8 est bien en racine ou cest une faute de frappe ? Sinon ça fait 2x^2-16x=0

Bin c'est bien ce que je pensais, oui n'est pas dans la racine car la formule d'origine pour le périmètre c'est p(x)= 8 + Racine de (2x²-16x+64)

Désolé j'arrive pas à faire le symbole racine carré

par **numero1** » 28 Nov 2015, 12:13

lop a écrit:En élevant au carré tu as :
2x^2-16x+64-8=0
Tu enlèves juste la racine
Mais est ce que 8 est bien en racine ou cest une faute de frappe ? Sinon ça fait 2x^2-16x=0

Donc comme 8 n'est pas dans la racine :
Racine de (2x²-16x+6) = 8

On a
2x²-16x+6 = 8

par **lop** » 28 Nov 2015, 12:14

Ah donc tu as ça,

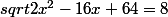
Tu élèves au carré,

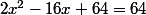
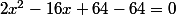
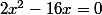
tu calcules delta et tu as tes deux solutions je pense.

par **numero1** » 28 Nov 2015, 12:16

lop a écrit:Ah donc tu as ça,

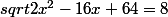
Tu élèves au carré,

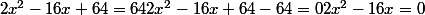
tu calcules delta et tu as tes deux solutions je pense.

Comment vous avez trouver 642x² ?

par **lop** » 28 Nov 2015, 12:17

numero1 a écrit:Comment vous avez trouver 642x² ?

Y'a eut une erreur d'affichage regarde mon message je l'ai modifié

Tu es en quel classe ? tu as vu comment calculer le discriminant ou pas encore ?

par **numero1** » 28 Nov 2015, 12:19

lop a écrit:Y'a eut une erreur d'affichage regarde mon message je l'ai modifié

D'accord merci

Delta = b²-4ac = 16² - 4x(2x0) = 256
c'est bien ?

256> 0
donc 2 solutions ?

par **lop** » 28 Nov 2015, 12:24

Oui c'est ça.

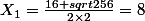
Tu as les deux racines.

par **numero1** » 28 Nov 2015, 12:24

lop a écrit:Oui c'est ça.

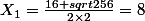
Tu as les deux racines.

Daccord merci beaucoup

par **lop** » 28 Nov 2015, 12:27

numero1 a écrit:Daccord merci beaucoup

De rien,
d'ailleurs

on voit bien que si tu remplaces par 8 et 0 ça marche

:ptdr:

Bonne aprem !

par **numero1** » 28 Nov 2015, 12:38

lop a écrit:De rien,
d'ailleurs
on voit bien que si tu remplaces par 8 et 0 ça marche :ptdr:

Bonne aprem !

Ah oui d'accord !!! :zen: :+++:
Bon aprèm !! :we: :lol3:

par **Carpate** » 28 Nov 2015, 12:55

lop a écrit:Ah donc tu as ça,

Tu élèves au carré,

tu calcules delta et tu as tes deux solutions je pense.

C'est aberrant de calculer le discriminant pour résoudre :

par **lop** » 28 Nov 2015, 13:01

Effectivement, j'avais pas trop réfléchis j'ai vu x^2 je me suis dit discriminant :)

Variation équation

variation équation

Qui est en ligne