DM forme canonique 2 ex

[Titanesque]

Bonjour,

Je sèche un peu pour un DM de mathématiques, est-ce que quelqu'un pourrait m'aiguiller sur les démarches à suivre ?

I- A=(4;-7/2) B=(1;-5/28) et C=(-2;-19/14) appartiennent à une parabole, déterminer la fonction associée.

II- 3 points distincts d'une parabole peuvent-ils être alignés ? Justifier.


Voilà le peu de réflexion que j'ai réussi à fournir :

I - a+b+c= -5/28
16a+4b+c=-7/2=-98/28
4a-2b+c=-19/4=-133/28

Et à près je n'arrive pas à trouver la manière la plus judicieuse pour découvrir mes trois inconnues.
J'ai l'impression de tourner en rond. J'ai des égalités comme 10a+b+c=-231/56, et j'ai vraiment l'impression de tout me compliquer plus qu'autre chose...

II- Pour la deuxième je pensais prouver que c'est impossible en utilisant ce que j'avais appris sur les fonctions affines.
Comme quoi la représentation graphique d'une fco affine est une droite, et qu'ainsi tous les points appartenant à cette droite sont alignés et ont le même coefficient directeur ->a.
a= Yb-Ya/Xb-Xa.
Et que si je calcule les coeff. directeurs de mes trois coordonnées et qu'elles ne sont pas similaires alors le points ne sont pas alignés. Puis je me suis rendue compte que c'est stupide car on retrouve un "a" dans la fonction de degré 2 et que je ne pense pas pouvoir admettre de conjecture.

[capitaine nuggets]

Bonjour,

Je sèche un peu pour un DM de mathématiques, est-ce que quelqu'un pourrait m'aiguiller sur les démarches à suivre ?

I- A=(4;-7/2) B=(1;-5/28) et C=(-2;-19/14) appartiennent à une parabole, déterminer la fonction associée.



Voilà le peu de réflexion que j'ai réussi à fournir :

I - a+b+c= -5/28
16a+4b+c=-7/2=-98/28
4a-2b+c=-19/4=-133/28

Et à près je n'arrive pas à trouver la manière la plus judicieuse pour découvrir mes trois inconnues.
J'ai l'impression de tourner en rond. J'ai des égalités comme 10a+b+c=-231/56, et j'ai vraiment l'impression de tout me compliquer plus qu'autre chose...

I : Oui, c'est la bonne idée :+++:
Choisis la première équation et retire la membre à membre dans la seconde et la troisième pour faire disparaître les "c". Résous alors le système de deux équations à deux inconnues a et b obtenues :++:

[capitaine nuggets]

II- 3 points distincts d'une parabole peuvent-ils être alignés ? Justifier.


Voilà le peu de réflexion que j'ai réussi à fournir :


II- Pour la deuxième je pensais prouver que c'est impossible en utilisant ce que j'avais appris sur les fonctions affines.
Comme quoi la représentation graphique d'une fco affine est une droite, et qu'ainsi tous les points appartenant à cette droite sont alignés et ont le même coefficient directeur ->a.
a= Yb-Ya/Xb-Xa.
Et que si je calcule les coeff. directeurs de mes trois coordonnées et qu'elles ne sont pas similaires alors le points ne sont pas alignés. Puis je me suis rendue compte que c'est stupide car on retrouve un "a" dans la fonction de degré 2 et que je ne pense pas pouvoir admettre de conjecture.

A vue de nez, j'aurai essayé deux choses :

Une parabole admet pour équation générale , .
Ensuite, je prendrais 3 points de cette parabole : .
J'aurais dit que A,B et C sont aligné si et seulement si l'un d'entre eux (B mettons) appartient à [AC]. Tu peux alors essayer de montrer que B n'appartient pas à la parabole.

(ou alors j'aurais tenté de calculer alors les coefficients directeur des droites (AB) et (BC) pour montrer qu'elles ne peuvent être parallèles...).

[Titanesque]

Merci,

J'ai réussi le I, et j'ai vérifié que l'image de 4 par ma fonction était bien -7/2. Alors merci de m'avoir permis d'y arriver :)

Quant au II je reconnais sécher encore mais je vais réfléchir à vos deux pistes.

[Carpate]

Merci,

J'ai réussi le I, et j'ai vérifié que l'image de 4 par ma fonction était bien -7/2. Alors merci de m'avoir permis d'y arriver

Quant au II je reconnais sécher encore mais je vais réfléchir à vos deux pistes.

D'une manière générale, les abscisses des points d'intersection d'une parabole d'équation y=ax^2+bx+c et d'une droite d'équation sont racines de l'équation du second degré :
Quel est le nombre maximum de racines d'une équation du second degré ?

[Ben314]

Salut,
La méthode de Carpate est (de loin) la plus simple (à la rigueur, si on veut être archi carré, il faut aussi mettre un vague mot concernant les droites d'équation x=Cst, mais c'est vite traité).

Mais ta méthode :

Comme quoi la représentation graphique d'une fco affine est une droite, et qu'ainsi tous les points appartenant à cette droite sont alignés et ont le même coefficient directeur ->a.
a= Yb-Ya/Xb-Xa.
Et que si je calcule les coeff. directeurs de mes trois coordonnées et qu'elles ne sont pas similaires alors le points ne sont pas alignés. Puis je me suis rendue compte que c'est stupide car on retrouve un "a" dans la fonction de degré 2 et que je ne pense pas pouvoir admettre de conjecture.

marcherais aussi (avec plus de calculs) :

Si on a une parabole d'équation y=ax²+bx+c (avec a non nul) et trois point différents , et alors :

Le coeff. directeur de la droite est vu que

De même, le coeff. directeur de la droite est

Les 3 points sont alignés ssi les deux coeff. directeurs sont les mêmes, c'est à dire c'est à dire ce qui, vu que a est non nul, signifie que 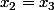: absurde.

[mathelot]

soient deux vecteurs



et sont colinéaires si et seulement si





conclusion:trois points distincts d'une parabole ne sont pas alignés