Explication sur la forme canonique

[Luc]

c'était une faute de frappe désolé.... je comprends toujours pas ... :/

Ok.
Voici comment procéder si tu ne connais pas la forme canonique. On développe l'expression
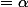
pour qu'elle soit égale à ce que tu veux. L'avantage de la forme canonique est que comme un carré est toujours positif, la hauteur maximale est atteinte quand x (car a va se révéler négatif), et cette hauteur vaut donc .
Développons donc :

donc

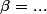
[elena22]

Ok.
Voici comment procéder si tu ne connais pas la forme canonique. On développe l'expression
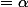
pour qu'elle soit égale à ce que tu veux. L'avantage de la forme canonique est que comme un carré est toujours positif, la hauteur maximale est atteinte quand x (car a va se révéler négatif), et cette hauteur vaut donc .
Développons donc :

donc

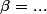
je crois que j'ai du passer trop de temps a essayer de chercher la réponse, depuis le début de l'après midi je suis dessus ! je comprends plus rien .... je suis désolée de paraitre... incompréhensible....
mais... je comprends pas vraiment comment on peut développer la forme canonique alors que l'on ne l'a pas !

[Luc]

je crois que j'ai du passer trop de temps a essayer de chercher la réponse, depuis le début de l'après midi je suis dessus ! je comprends plus rien .... je suis désolée de paraitre... incompréhensible....
mais... je comprends pas vraiment comment on peut développer la forme canonique alors que l'on ne l'a pas !

En fait on cherche a, , et pour que l'on ait .
Si l'on développe le carré, et que l'on remplace par sa définition, on obtient :
.
On peut ensuite identifier les coefficients un par un : on obtient donc
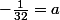
(coefficient en )
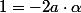
(coefficient en )
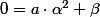
.(coefficient constant)

Tu peux résoudre ces équations pour obtenir successivement , et .

[elena22]

Ok.
Voici comment procéder si tu ne connais pas la forme canonique. On développe l'expression
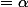
pour qu'elle soit égale à ce que tu veux. L'avantage de la forme canonique est que comme un carré est toujours positif, la hauteur maximale est atteinte quand x (car a va se révéler négatif), et cette hauteur vaut donc .
Développons donc :

donc

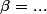
on a pas l'équation au complet pourtant dans l'énoncé !... je rame !

[elena22]

En fait on cherche a, , et pour que l'on ait .
Si l'on développe le carré, et que l'on remplace par sa définition, on obtient :
.
On peut ensuite identifier les coefficients un par un : on obtient donc
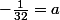
(coefficient en )
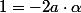
(coefficient en )
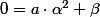
.(coefficient constant)

Tu peux résoudre ces équations pour obtenir successivement , et .

je crois enfin comprendre ! merci beaucoup !!!

[Luc]

je crois enfin comprendre ! merci beaucoup !!!

Ça vaut la peine de comprendre cette notion, tu la retrouveras tant en maths qu'en physique et en chimie pendant tout le lycée et même après. :lol3:

[elena22]

Ça vaut la peine de comprendre cette notion, tu la retrouveras tant en maths qu'en physique et en chimie pendant tout le lycée et même après. :lol3:

dans ce cas la c'est sur je pense qu'on va aprofondir en cours !!! ca devait etre un exercice d'approche !

[Carpate]

je crois enfin comprendre ! merci beaucoup !!!

Et, ce qui revient au même que la méthode de Luc :
En partant de la forme canonique obtenue dans un de mes messages précédents :

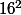
Cette expression est maximum quand la quantité que l'on soustrait au nombre positif est nulle soit pour

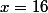
[lat36]

Bonjour à tous.

Il me semble que je rencontre un peu le même problème qu'elena22, en effet je suis aussi en 1eS et je dois passer d'un polynome du 2nd degré à la forme canonique. Or, j'ai
T(x)=-3x² + 2x -1/3. La correction a été donnée, mais je ne l'ai pas comprise! :cry:
c'était = -3 (x² - 1,5x)- 1/3
= -3 [(x-1/3)² - 1/9 ] -1/3
= -3 (x-1/3)

Pourriez vous m'expliquer pourquoi ?

Merci beaucoup de me répondre, il faudrait que je sache refaire ça pour demain !

[Carpate]

Bonjour à tous.

Il me semble que je rencontre un peu le même problème qu'elena22, en effet je suis aussi en 1eS et je dois passer d'un polynome du 2nd degré à la forme canonique. Or, j'ai
T(x)=-3x² + 2x -1/3. La correction a été donnée, mais je ne l'ai pas comprise!
c'était = -3 (x² - 1,5x)- 1/3
= -3 [(x-1/3)² - 1/9 ] -1/3
= -3 (x-1/3)

Pourriez vous m'expliquer pourquoi ?

Merci beaucoup de me répondre, il faudrait que je sache refaire ça pour demain !

Bonjour,
Ouvre un nouveau fil de discussion au lieu de parasiter un post déjà en cours ...