Sens de variation suite

[helpmeplease8]

Bonsoir, je ne comprends pas trop l'énoncé de cet exercice :help: :
Dans chacun des cas suivants déterminer le sens de variation de la suite (un) définie pour tout n appartient à l'ensemble N par u(petit n) =f(n) en étudiant d'abord les variations de la fonction f :

a) un= racine carré de 3n+4
b) un= -n^3 + 4n^2 - 5n

Merci :help:

[capitaine nuggets]

Salut !

Dans les deux cas, tu peux étudier le signe de la différence .
Je te rappelle la formule de "conjugaison" pour le 1), quels que soient :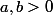

[CENTER]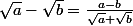[/CENTER]

[helpmeplease8]

Salut !

Dans les deux cas, tu peux étudier le signe de la différence .
Je te rappelle la formule de "conjugaison" pour le 1), quels que soient :

[CENTER][/CENTER]

d'accord merci, donc si je comprends bien dans cet exercice il ne s'agit pas de tableau de variation de fonction mais seulement de la différence de un - un+1 ?

[Shew]

d'accord merci, donc si je comprends bien dans cet exercice il ne s'agit pas de tableau de variation de fonction mais seulement de la différence de un - un+1 ?

Ca ou on pose et dans ce cas la on étudie la variation de f(x) .

[helpmeplease8]

Ca ou on pose et dans ce cas la on étudie la variation de f(x) .

ça m'a l'air plus simple d'étudier la variation de f(x) en posant un=f(n) , pour le deuxième cas je dois dériver la fonction pour aboutir à du second degré ? :help:

[capitaine nuggets]

ça m'a l'air plus simple d'étudier la variation de f(x) en posant un=f(n) , pour le deuxième cas je dois dériver la fonction pour aboutir à du second degré ? :help:

Ca peut-être plus simple dans ces cas là, mais tu peux tomber sur des cas plus tordus.

Pour 2), pas la peine de dériver : les termes en s'annulent :+++: