Forme canonique

[Dwayne]

Bonjour j'ai un problème avec cette exercice

La parabole ci contre représente une fonction f définie par: x --> (x-a)^2+m.

1. Quelles sont les coordonnées du sommet de la parabole?
2.Déduisez en l'expression de f(x).

la photo [url=http://]http://www.ilemaths.net/img/forum_img/0637/forum_637653_1.jpg[/url]

j'ai répondu
1) (2;-2)
2, (x-2)^2-2

mais justement, je me demande si il y a un calcul qui se cache quelque part ... cette exercice est du livre 87 page 83 de transmath seconde programme 2010

[Pseuda]

Bonjour j'ai un problème avec cette exercice

La parabole ci contre représente une fonction f définie par: x --> (x-a)^2+m.

1. Quelles sont les coordonnées du sommet de la parabole?
2.Déduisez en l'expression de f(x).

la photo [url=http://]http://www.ilemaths.net/img/forum_img/0637/forum_637653_1.jpg[/url]

j'ai répondu
1) (2;-2)
2, (x-2)^2-2

mais justement, je me demande si il y a un calcul qui se cache quelque part ... cette exercice est du livre 87 page 83 de transmath seconde programme 2010

Bonjour,

Le sommet de la parabole est le point où passe le minimum ou le maximum de la fonction (selon le signe du coefficient de x^2). Ici c'est un minimum.

Pour quelle valeur de x a-t-on le minimum de (x-a)^2 + m ? d'où tu tires l'ordonnée du point ensuite.

[capitaine nuggets]

Même si cette fonction peut paraître balèze, il n'en est rien.

1) En fait, si tu regardes bien (avec la calculatrice éventuellement), n'est qu'une la translation de la fonction "carré" 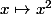par le vecteur .

Autrement dit :
Soient et les courbes représentatives respectives de la fonctions et de la fonction "carré".

Les coordonnées du sommet de sont obtenu lorsque . Donc finalement le sommet de a pour coordonnées . Maintenant, on sait que est un "déplacement" de la courbe (graphiquement de unités vers la droite et de unités vers le haut), donc sont sommet a pour coordonnées ... :+++: