Etude de dérivabilité
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Vados
- Membre Relatif
- Messages: 216
- Enregistré le: 21 Avr 2014, 18:46
-
 par Vados » 04 Nov 2014, 20:42
par Vados » 04 Nov 2014, 20:42
Bonsoir! Pourrais-je avoir de l'aide pour cette exercice s'il vous plaît ?
 On souhaite étudier la dérivabilité des fonctions cos et sin sur R
On souhaite étudier la dérivabilité des fonctions cos et sin sur R
1)Soit a appartient à R et h non nul
Calculer le taux d'accroissement [sin(a+h)- sin(a)] / h en fonction de sin(a) , cos(a) , sin(h) , cos(h) et h .
En déduire la dérivabilité de sin en a et donner la valeur du nombre dérivé sin'(a)J'en suis arrivé à [ [sin(a)*cos(h) + cos(a)*sin(h)] - sin(a) ] / h
-
Vados
- Membre Relatif
- Messages: 216
- Enregistré le: 21 Avr 2014, 18:46
-
 par Vados » 04 Nov 2014, 21:44
par Vados » 04 Nov 2014, 21:44
Alors s'il vous plaît?
-
Vados
- Membre Relatif
- Messages: 216
- Enregistré le: 21 Avr 2014, 18:46
-
 par Vados » 04 Nov 2014, 23:10
par Vados » 04 Nov 2014, 23:10
Personne pour m'aider ? c'est assez urgent...
-
mathelot
 par mathelot » 04 Nov 2014, 23:31
par mathelot » 04 Nov 2014, 23:31
-
Vados
- Membre Relatif
- Messages: 216
- Enregistré le: 21 Avr 2014, 18:46
-
 par Vados » 05 Nov 2014, 16:37
par Vados » 05 Nov 2014, 16:37
J'ai pas tout compris...

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 05 Nov 2014, 16:47
par zygomatique » 05 Nov 2014, 16:47
Vados a écrit:J'ai pas tout compris...
salut
normal ...
car tout le problème est de savoir ce que tu sais sur ces fonctions ....
et sans la connaissance d'un résultat on ne peut s'en sortir ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 05 Nov 2014, 16:52
par Carpate » 05 Nov 2014, 16:52
Vados a écrit:J'ai pas tout compris...
Variante en utilisant la bonne vieille formule d'addition (connue des élèves de nos jours ?) :
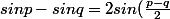 cos( \frac{p+q}{2}))
avec p =a+h et q= a
=\frac{sin(a+h)-sina}{h} =\frac{2sin(\frac{h}{2})cos(a+\frac{h}{2})}{h})
=\frac{sin(\frac{h}{2})}{\frac{h}{2}} cos(a+\frac{h}{2}))
etc ...
-
Vados
- Membre Relatif
- Messages: 216
- Enregistré le: 21 Avr 2014, 18:46
-
 par Vados » 05 Nov 2014, 17:19
par Vados » 05 Nov 2014, 17:19
On ne pourrait continuer par rappart à ce que je fais?

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 05 Nov 2014, 17:52
par zygomatique » 05 Nov 2014, 17:52
Carpate a écrit:Variante en utilisant la bonne vieille formule d'addition (connue des élèves de nos jours ?) :
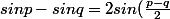 cos( \frac{p+q}{2}))
avec p =a+h et q= a
=\frac{sin(a+h)-sina}{h} =\frac{2sin(\frac{h}{2})cos(a+\frac{h}{2})}{h})
=\frac{sin(\frac{h}{2})}{\frac{h}{2}} cos(a+\frac{h}{2}))
etc ...
ce qui nécessite à nouveau de connaître un certain résultat particulier ....
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Vados
- Membre Relatif
- Messages: 216
- Enregistré le: 21 Avr 2014, 18:46
-
 par Vados » 05 Nov 2014, 18:43
par Vados » 05 Nov 2014, 18:43
Vous n'avez pas répondu à ma question ....
-
Vados
- Membre Relatif
- Messages: 216
- Enregistré le: 21 Avr 2014, 18:46
-
 par Vados » 05 Nov 2014, 19:54
par Vados » 05 Nov 2014, 19:54
Alors s'il vous plaît
-
Vados
- Membre Relatif
- Messages: 216
- Enregistré le: 21 Avr 2014, 18:46
-
 par Vados » 05 Nov 2014, 20:26
par Vados » 05 Nov 2014, 20:26
C'est assez urgent !
-
Vados
- Membre Relatif
- Messages: 216
- Enregistré le: 21 Avr 2014, 18:46
-
 par Vados » 05 Nov 2014, 21:08
par Vados » 05 Nov 2014, 21:08
est-ce qu'il y a quelqu'un sur ce forum qui pourrait m'apporter une aide sérieusement ^^ ?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 05 Nov 2014, 21:14
par Carpate » 05 Nov 2014, 21:14
Vados a écrit:est-ce qu'il y a quelqu'un sur ce forum qui pourrait m'apporter une aide sérieusement ^^ ?
Il semblerait que l'on montre dans le secondaire par une méthode géométrique (pas très rigoureuse paraît-il) que :


A partir de cela, l'affaire est dans le sac ...
-
Vados
- Membre Relatif
- Messages: 216
- Enregistré le: 21 Avr 2014, 18:46
-
 par Vados » 05 Nov 2014, 21:35
par Vados » 05 Nov 2014, 21:35
Je n'en suis qu'à ça : [ [sin(a)*cos(h) + cos(a)*sin(h)] - sin(a) ] / h !
-
gab33
- Messages: 2
- Enregistré le: 05 Nov 2014, 20:45
-
 par gab33 » 05 Nov 2014, 21:41
par gab33 » 05 Nov 2014, 21:41
-
Vados
- Membre Relatif
- Messages: 216
- Enregistré le: 21 Avr 2014, 18:46
-
 par Vados » 05 Nov 2014, 21:52
par Vados » 05 Nov 2014, 21:52
bouge , qu'est tu fais la ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 06 Nov 2014, 01:11
par Ben314 » 06 Nov 2014, 01:11
Carpate a écrit:Il semblerait que l'on montre dans le secondaire par une méthode géométrique (pas très rigoureuse paraît-il) que :

Effectivement, pour arriver à ça comme résultat, la méthode a de forte chance de ne "pas être très rigoureuse"... :dingue2:
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 06 Nov 2014, 08:22
par Carpate » 06 Nov 2014, 08:22
Ben314 a écrit:Effectivement, pour arriver à ça comme résultat, la méthode a de forte chance de ne "pas être très rigoureuse"... :dingue2:
-1}{h}=0)
Décidément j'enchaîne les coquilles !
Donc pour Vados, s'il n'a pas déjà rendu son exercice.
"Je n'en suis qu'à ça : [ [sin(a)*cos(h) + cos(a)*sin(h)] - sin(a) ] / h !"Factorise par sin(a) :
-sin(a)}{h}=\frac{cos(h) -1}{h} sin(a) + cos(a) \frac{sin(h)}{h})
)'=cos(x))
-
mathelot
 par mathelot » 06 Nov 2014, 13:20
par mathelot » 06 Nov 2014, 13:20
Carpate a écrit:)'=cos(x))
)^'= 0)
, non ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 49 invités
