Applications linéaires

[Victhemath]

Bonsoir, des deux exercices à faire pour demain. Mon cours venant d'être étudié dans la journée, j'ai pas pu encore tout assimiler pour réussir ses deux exercices. Quelqu'un pour m'aider ?


Déterminer toutes les applications linéaires f : R^2 --> R^3 s'il en existe qui vérifient :
f =

et f =




2° exo : Déterminer toutes les applications linéaires f: Mn(K) --> Mn(K), s'il en existe, pour lesquelles une matrice antisymétrique a pour image son double et pour lesquelles une matrice symétrique a pour image son triple.

Merci

[zygomatique]

salut

que peut-on dire de la famille ((1, 2), (2, 1)) ?

[zygomatique]

toute matrice M s'écrit ::



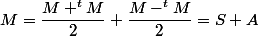
où S est symétrique et A est antisymétrique

et les espaces {S} et {A} sont supplémentaires

....

[Victhemath]

salut

que peut-on dire de la famille ((1, 2), (2, 1)) ?

On voit qu'elle est libre et génératrice. C'est une base et on a un théorème qui nous dit que toute application linéaire de f est entièrement et uniquement déterminée par ses valeurs sur les vecteurs de la base. Qu'est-ce que ça veut dire ?

toute matrice M s'écrit ::



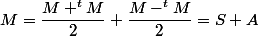
où S est symétrique et A est antisymétrique

et les espaces {S} et {A} sont supplémentaires

....

On peut dire que leur somme directe est l'ensemble Mn(K) est que leur intersection est vide mais du coup que si l'on connait f (d'un élément de la base) et la restriction de f à vect d'un l'élement de la base alors on connait f.
Même question que l'exo 1, je ne voies pas ...

[Robic]

on a un théorème qui nous dit que toute application linéaire de f est entièrement et uniquement déterminée par ses valeurs sur les vecteurs de la base. Qu'est-ce que ça veut dire ?

Ça veut dire que c'est bon, on la connaît, il y en a une et une seule. Bref : si on te donne les images des vecteurs de base, alors il y a une unique application linéaire qui correspond.

C'est le cas dans cet exercice. Reste à « déterminer » cette application linéaire. Je suppose qu'il s'agit de l'écrire sous forme f(x;y) = (ax + by ; cx + dy ; ex + fy). Ou peut-être sous forme de matrice. Pour ça, il faudra trouver f(i) et f(j) (où i et j sont les vecteurs de la base canonique) et ça se détermine à l'aide de f(1;2) et f(2;1). Comment ? En n'oubliant pas que f(1;2) = f(1;0) + f(0;2) = f(i) + 2 f(j) et ainsi de suite.

(J'ai écrit les vecteurs en ligne parce que c'est plus facile ici, j'espère que ça reste compréhensible. De toute façon l'écriture en ligne doit aussi être connue.)

[Victhemath]

une fois avoir trouver les vecteurs f(i) et f(j), je fais quoi ?

[Robic]

Eh ben c'est fini !

On demandait de déterminer f. En fait, on pouvait peut-être s'arrêter après avoir lu l'énoncé : f est entièrement déterminée par les images de (1;2) et (2;1), j'ai fini, basta ! Mais à mon avis il faut en faire un petit peu plus.

Avec les images de f(i) et f(j), tu peux calculer l'image d'un (x;y) quelconque.
On a en effet, par linéarité : f(x;y) = x f(i) + y f(j),
du coup ça permet d'exprimer (x';y';z') en fonction de (x;y) par quelque chose de la forme :
x' = ax + by
y' = cx + dy
z' = ex + fy,
ou bien on peut l'écrire sous forme matricielle (lignes ab, cd, ef).

[zygomatique]

oui on peut s'arrêter directement aux vecteurs donnés dans l'énoncé ...

puisque tout vecteur s'écrit de façon unique x(1, 2) + y(2, 1) ....