Pour les ambitieux :D (polynome)
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
bneay
- Membre Naturel
- Messages: 53
- Enregistré le: 06 Jan 2014, 23:04
-
 par bneay » 18 Mar 2014, 19:34
par bneay » 18 Mar 2014, 19:34
Salut tout le monde; j'ai une question pour les ambitieux d'entre vous^^
existe-t-l une suite
)
(n>= 0) tq pour tout entier naturel n, le polynome:

ademet exactement n racines distinctes.
Amusez vous Matheux :we:
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 18 Mar 2014, 20:09
par Doraki » 18 Mar 2014, 20:09
1,1,1,1,1,1,1,1 ....
1+x+x²+...+x^n = (x^(n+1) - 1)/(x-1), qui a bien n racines distinctes dans C.
J'ai gagné quoi ?
-
wserdx
- Membre Rationnel
- Messages: 654
- Enregistré le: 03 Oct 2009, 13:44
-
 par wserdx » 18 Mar 2014, 20:36
par wserdx » 18 Mar 2014, 20:36
Doraki a écrit:1,1,1,1,1,1,1,1 ....
1+x+x²+...+x^n = (x^(n+1) - 1)/(x-1), qui a bien n racines distinctes dans C.
J'ai gagné quoi ?
Bah, dans

les racines, non ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 18 Mar 2014, 20:37
par Ben314 » 18 Mar 2014, 20:37
Salut,
C'est trés trés trés con comme question :
Si tu tire totalement au pif un polynôme de degré n dans C, ben le cas "exeptionnel", c'est qu'il ait une racines doubles (ou plus) et le cas de trés loin le plus fréquent c'est qu'il ait des racines distinctes.
- Au sens de la mesure, les polynômes n'ayant pas n racines simples sont de mesure nulle.
- Au sens de la topologie, c'est un ensemble d'intérieur vide.
- Au sens des variétés, c'est (presque partout) une variété de dimension strictement inférieure à celle des polynômes de degrés n.
Aprés, par contre, c'est dans l'autre sens que ça me semble pas clair du tout :
Existe t'il une suite de complexes tous non nuls (y'a qu'à dire... pour éviter que la suite stagne) tel que tes fameux polynômes aient tous (au minimum) une racine double ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 18 Mar 2014, 20:38
par Ben314 » 18 Mar 2014, 20:38
wserdx a écrit:Bah, dans

les racines, non ?
Heuuu, c'était précisé où dans l'énoncé le "dans R" ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 18 Mar 2014, 20:48
par Ben314 » 18 Mar 2014, 20:48
Si le problème est dans R, c'est plus interessant, mais... pas trés dur :
On construit les An par récurence et il suffit de voir que, si on a un polynôme de degrés n, en ajoutant epsilon.X^(n+1) on change systématiquement de signe pour une des deux limites en +oo ou -oo mais que, si on prend epsilon suffisement petit, on ne va pas changer les signes des P(x) pour les extrémums locaux du polynôme (i.e. les racines de la dérivée).
Résultat : on créera forcément une racine suplémentaire (réelle) distincte des autres.
Aprés, si on veut une "vrai" valeur pour les An, il suffit de les prendre qui diminuent "trés trés vite" pour arriver à montrer que ça marche.
Mais ça risque d'être chiant et c'est inutile vu que la question est uniquement "existe t'il..." et pas "exhiber..."
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
bneay
- Membre Naturel
- Messages: 53
- Enregistré le: 06 Jan 2014, 23:04
-
 par bneay » 19 Mar 2014, 09:28
par bneay » 19 Mar 2014, 09:28
Ben314 a écrit:Si le problème est dans R, c'est plus interessant, mais... pas trés dur :
On construit les An par récurence et il suffit de voir que, si on a un polynôme de degrés n, en ajoutant epsilon.X^(n+1) on change systématiquement de signe pour une des deux limites en +oo ou -oo mais que, si on prend epsilon suffisement petit, on ne va pas changer les signes des P(x) pour les extrémums locaux du polynôme (i.e. les racines de la dérivée).
Résultat : on créera forcément une racine suplémentaire (réelle) distincte des autres.
Aprés, si on veut une "vrai" valeur pour les An, il suffit de les prendre qui diminuent "trés trés vite" pour arriver à montrer que ça marche.
Mais ça risque d'être chiant et c'est inutile vu que la question est uniquement "existe t'il..." et pas "exhiber..."
Alors Mr Ben, quelle suite proposez vous? après avoir fini votre récurrence? c'est exhiber mnt! (Enfin de compte on travaille dans IR[X] pas dans C[X], je m'excuse car je l'ai pas signalé)
-
Robic
- Membre Irrationnel
- Messages: 1084
- Enregistré le: 03 Mai 2013, 11:00
-
 par Robic » 19 Mar 2014, 10:55
par Robic » 19 Mar 2014, 10:55
Une idée intuitive, c'est de partir du développement en série du cosinus. J'ai déjà vu le dessin des courbes des polynômes correspondant aux premiers coefficients, et ça donne autant de racines que le degré. Par exemple x-->1-x²/2 a deux racines et x-->1-x²/2+x^4/4! en a quatre. Bon, ce n'est pas une démonstration, mais je serais surpris que ce soit faux.
Du coup la suite serait :
^k}{(2k)!})
et
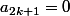
.
Cette suite se comporte comme l'a indiqué Ben314 : en diminuant très vite.
(Par contre ce n'est pas le polynôme

qui admet n racines, juste le polynôme

. Ah, zut... Mais bon, à part ce détail sans importance il me semble que l'essentiel est trouvé.)

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 19 Mar 2014, 11:43
par chan79 » 19 Mar 2014, 11:43
Robic a écrit:Une idée intuitive, c'est de partir du développement en série du cosinus. J'ai déjà vu le dessin des courbes des polynômes correspondant aux premiers coefficients, et ça donne autant de racines que le degré. Par exemple x-->1-x²/2 a deux racines et x-->1-x²/2+x^4/4! en a quatre. Bon, ce n'est pas une démonstration, mais je serais surpris que ce soit faux.
Du coup la suite serait :
!})
et
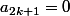
.
Cette suite se comporte comme l'a indiqué Ben314 : en diminuant très vite.
(Par contre ce n'est pas le polynôme

qui admet n racines, juste le polynôme

. Ah, zut... Mais bon, à part ce détail sans importance il me semble que l'essentiel est trouvé.)
En allant jusqu'à 6, il ne doit y avoir que deux racines réelles
=1-\fra{x^2}{2!}+\fra{x^4}{4!}-\fra{x^6}{6!})

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 19 Mar 2014, 17:23
par Ben314 » 19 Mar 2014, 17:23
Une solution pas trop compliquée :
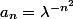
avec

fixé :
Pour tout

(donc n+1 valeurs) on a
^pP_n(-\lambda^{2p})\ =\ \lambda^{p^2}\sum_{k=0}^n(-1)^{k+p}\lambda^{-k^2+2pk-p^2}\ =\ \lambda^{p^2}\sum_{i=-p}^{n-p}(-1)^i\lambda^{-i^2}\geq \lambda^{p^2}(1-2\lambda^{-1})\ >\ 0)
Donc

admet

alternances de signes successives : il s'anule

fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Robic
- Membre Irrationnel
- Messages: 1084
- Enregistré le: 03 Mai 2013, 11:00
-
 par Robic » 19 Mar 2014, 18:20
par Robic » 19 Mar 2014, 18:20
chan79 a écrit:En allant jusqu'à 6, il ne doit y avoir que deux racines réelles
=1-\fra{x^2}{2!}+\fra{x^4}{4!}-\fra{x^6}{6!})
Zut, je viens de vérifier, tu as raison...

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 20 Mar 2014, 13:29
par zygomatique » 20 Mar 2014, 13:29
salut
soit

une suite strictement croissante de réels
posons
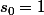



....
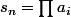
alors le polynome
 = \sum_0^n (-1)^ks_{n-k}x^k)
admet les racines

...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 20 Mar 2014, 13:30
par zygomatique » 20 Mar 2014, 13:30
ouais en fait je ne répond pas vraiment au problème .... :hum:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
bneay
- Membre Naturel
- Messages: 53
- Enregistré le: 06 Jan 2014, 23:04
-
 par bneay » 20 Mar 2014, 14:24
par bneay » 20 Mar 2014, 14:24
zygomatique a écrit:ouais en fait je ne répond pas vraiment au problème .... :hum:
tu as construit une nouvelle suite de coefficients, à l'aide de la formule de Viète bien évidemment, de telle façons que les ai sont les racines de P, et de telle façon que P soit scindé dans IR..
Mais comme tu l'as dit, c'est pas ce qu'on cherche, malheureusement!
-
Robic
- Membre Irrationnel
- Messages: 1084
- Enregistré le: 03 Mai 2013, 11:00
-
 par Robic » 20 Mar 2014, 15:36
par Robic » 20 Mar 2014, 15:36
(Ah, zut, j'avais trouvé un truc intéressant mais ça ne répond pas du tout à la question...)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 19 invités
et
.
qui admet n racines, juste le polynôme
. Ah, zut... Mais bon, à part ce détail sans importance il me semble que l'essentiel est trouvé.)