Factorisation d'un polynome

[Subitus]

Bonjour, je reprends les études et je révise un programme de 1ère, Terminale S.
Je bloque sur un exercice où j'ai remarqué plusieurs fois la même méthode de résolution dans la correction mais je ne peux me l'expliquer.
J'ai :
x²+x-2 = (x-1)(x+2)

Comment obtiens t-on cette factorisation, est-ce une identité remarquable ?
Il est précisé que le calcul du discriminant nous permet de factoriser l'expression ci-desssus. Je ne vois pas comment.

De même mais dans un autre registre pour :

x²-4x+3 = (x-2)² -4 +3
Est-ce le même type de calcul ?

Merci de votre aide et j'espère avoir été assez clair et concis.

[ampholyte]

Bonjour,

Tous les polynômes peuvent s'écrire sous la forme factorisée :

ax² + bx + c = a(x - x1) (x - x2) avec x1 et x2 les racines du polynômes.

Dans ton exemple, il faut calculer les racines :

On résout :
x² + x - 2 = 0



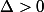donc il existe deux racines réelles :





D'où le résultat :
x² + x - 2 = (x - x1)(x - x2) = (x - 1)(x + 2)

Pour ton second problème, c'est ce que l'on appelle la forme canonique. On va chercher à factoriser directement le polynome.

x² - 4x + 3 = (x² - 4x) + 3
= (x² - 4x + 4) - 4 + 3 => On essaye de retomber sur une identité remarquable
= (x - 2)² - 4 + 3
= (x - 2)² - 1
= (x - 2 - 1)(x - 2 + 1) => a² - b² = (a - b)(a + b)
= (x - 3)(x - 1)

[Cliffe]

Tu peux faire ça aussi :

[CENTER] [/CENTER]

[capitaine nuggets]

Bonjour,

Tous les polynômes peuvent s'écrire sous la forme factorisée :

ax² + bx + c = (x - x1) (x - x2) avec x1 et x2 les racines du polynômes.

Dans ton exemple, il faut calculer les racines :

On résout :
x² + x - 2 = 0



donc il existe deux racines réelles :





D'où le résultat :
x² + x - 2 = (x - x1)(x - x2) = (x - 1)(x + 2)

Attention à l'oubli du "" : .
Là ca marche car , mais si on avait , ça n'aurait pas été le cas. Un exemple : bien que les trinômes du second degré et aient même racines, il n'ont pas même factorisation :we:

[ampholyte]

Attention à l'oubli du "" : .
Là ca marche car , mais si on avait , ça n'aurait pas été le cas. Un exemple : bien que les trinômes du second degré et aient même racines, il n'ont pas même factorisation :we:

Oui en effet, coquille de ma part, je corrige .

[Subitus]

Merci pour votre aide, j'ai bien compris
Bonne journée

[Subitus]

En fait, je pensais pas en arrivé la mais je suis maintenant confronté à un polynôme de degré supérieur pour une factorisation.

f(x)= x^3+2x²-x-2 .

il est dit : On calcule f(1)=0 ce qui permet de factoriser sous la forme f(x)= (x-1)(ax²+bx+c)

Quel est l'intérêt de calculer f(1) ? Et quel est la relation entre cette forme et les polynômes de degré 3 ?
A savoir que l'exercice est conçu pour une étude de signe de la fonction.

Merci d'avance

[ampholyte]

En fait, chaque polynôme peut se factoriser par le produit de ces racines.

Comme il est plus difficile de résoudre une équation du 3eme degré, on recherche très souvent un ou plusieurs racines évidentes (ici le calcul de f(1) = 0, te donne la solution évidente x = 1)

On peut donc factoriser f(x) par sa première racine c'est à dire f(x) = x³ + 2x² - x + 2 = (x - 1)(ax² + bx + c). Avec a, b et c que tu dois déterminer (en redéveloppant l'expression).

Une fois que tu auras la véritable expression de f(x), il te suffira de factoriser le polynôme du second degré afin d'obtenir la forme factorisée suivante :

f(x) = a(x - 1)(x - x1)(x - x2) avec x1 et x2 les racines du polynôme du second degré que tu auras obtenu.

Cela te permet d'avoir ton tableau de signe rapidement.

Autre solution : si tu as déjà étudié le signe d'un polynôme du second degré, tu peux directement étudier le signe de f(x) sous la forme (x - 1)(ax² + bx + c).

[Subitus]

Merci de votre aide, j'ai compris :)