Eq diff
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
express
- Messages: 3
- Enregistré le: 13 Mar 2014, 10:42
-
 par express » 13 Mar 2014, 10:44
par express » 13 Mar 2014, 10:44

bonjour
comment peut t'on résoudre cette équation différentielle non linéaire ? j'ai essayé de poser x=sin(béta) de faire appel à des matrices
des séries mais j'ai pas trouver une solution
prière de m'aider et merci bien
(tous les termes sont constants sauf béta bien-sur)
-
Sourire_banane
- Membre Irrationnel
- Messages: 1355
- Enregistré le: 23 Juil 2013, 11:48
-
 par Sourire_banane » 13 Mar 2014, 11:56
par Sourire_banane » 13 Mar 2014, 11:56
express a écrit:
bonjour
comment peut t'on résoudre cette équation différentielle non linéaire ? j'ai essayé de poser x=sin(béta) de faire appel à des matrices
des séries mais j'ai pas trouver une solution
prière de m'aider et merci bien
(tous les termes sont constants sauf béta bien-sur)
Salut,
On fait appel à maple ou à tout autre logiciel de calcul numérique qui puisse nous faire du Euler ou du Runge-Kutta

-
express
- Messages: 3
- Enregistré le: 13 Mar 2014, 10:42
-
 par express » 13 Mar 2014, 13:27
par express » 13 Mar 2014, 13:27
Sourire_banane a écrit:Salut,
On fait appel à maple ou à tout autre logiciel de calcul numérique qui puisse nous faire du Euler ou du Runge-Kutta

mais j'ai besoin des étapes de calculs :mur: merci en tous cas :we:
-
Black Jack
 par Black Jack » 13 Mar 2014, 14:15
par Black Jack » 13 Mar 2014, 14:15
Première question a se poser : L'équation est-elle homogène ?
Pas facile de répondre sans connaître l'énoncé "physique" d'où elle provient, mais cela n'empêche pas d'y réfléchir.
Beta est un angle ou un arc ... donc sans dimension (à ne pas confondre avec sans unité, c'est fondamentalement différent)
et donc [d²Beta/dt²] = T^-2
on doit avoir : [a]=[c] et [w².a] = [mab]
--> [w²] = [mb]
on renifle que w est une pulsation, g une accélération et m une masse et donc : T^-2 = [b] * M
[b] = M^-1.T^-2
Et donc [mgb] = M.L.T^-2 * M^-1.T^-2 = L.T^-4 alors que cela devrait avoir les mêmes dimensions que d²Beta/dt², soit donc T^-2
Je mettrais ta tête à couper que l'équation n'est pas homogène ... et donc fausse.
Cela vaudrait la peine de vérifier avec les données physiques vraies (et pas les reniflées, comme je l'ai fait), mais je ne serais pas étonné qu'il y ait un cheveu dans le potage.
:zen:
 par busard_des_roseaux » 13 Mar 2014, 14:18
par busard_des_roseaux » 13 Mar 2014, 14:18
bonjour,
l'équation est de la forme
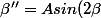+ B cos(\beta)+ C sin(\beta))
on mutiplie par
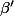
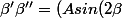+ B cos(\beta)+ C sin(\beta)) \beta')
ça se primitive
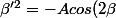 +2 B sin(\beta) - 2 C cos(\beta) + E)
on écrit la racine carrée
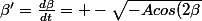 + 2B sin(\beta) - 2C cos(\beta) + E})
ensuite l'équation est dite à variable séparée
 + 2B sin(\beta) - 2C cos(\beta) + E}}=+- dt)
on cherche une primitive F du membre de gauche relativement à

on obtient
=t+G)
(1) où G est une constante d'intégration
ensuite , localement les courbes intégrales de (1) sont peut être des courbes représentatives
de fonction
)
, par le théorème d'inversion locale
-
Black Jack
 par Black Jack » 13 Mar 2014, 15:24
par Black Jack » 13 Mar 2014, 15:24
Si l'équation de départ est correcte (ce que je pense faux, si elle bien issue d'un problème de physique), j'arrive à un résultat analogue, par une autre méthode, à celui de busard_des_roseaux.
Mais pour exprimer Beta(t) à partir de l'équation à variables séparées à laquelle on aboutit ... bernique.
:zen:
-
express
- Messages: 3
- Enregistré le: 13 Mar 2014, 10:42
-
 par express » 13 Mar 2014, 20:48
par express » 13 Mar 2014, 20:48
merci pour les interventions
l'équation est issue d'un problème de mécanique générale
voila les dimensions
bêta est homogène à un angle
m:masse
a,b sont des longueurs
g accélération
A et C sont des moments d'inerties
w pulsation
-
Black Jack
 par Black Jack » 14 Mar 2014, 13:19
par Black Jack » 14 Mar 2014, 13:19
express a écrit:merci pour les interventions
l'équation est issue d'un problème de mécanique générale
voila les dimensions
bêta est homogène à un angle
m:masse
a,b sont des longueurs
g accélération
A et C sont des moments d'inerties
w pulsation
Et donc [mgb.sin(Beta)] = M * LT^-2 * L = ML²T^-2 (dimension d'une énergie)
et [d²Beta/dt²] n'a pas les dimensions d'une énergie.
L'équation n'est pas homogène et est donc fausse.
:zen:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités

