Eq. Diff : solution réelle et complexe

[greghowe]

Bonjour,

je souhaiterais savoir qu'elle est la relation entre la solution réelle et complexe d'une équation différentielle linéaire de degré quelconque pour des conditions initiales fixées. Plus précisement, sachant que la solution s'écrit comme combinaison linéaire d'exponentielles(en produit avec sin, cos dans le cas réelle), comment fait on pour retrouver les coefficients de la solution réelle à partir de ceux de la solution complexe.

Merci

[egan]

Il n'est pas obligatoire d'avoir une solution réelle. Typiquement, y'+iy=0. Ou alors un truc du genre y''+y=0 avec y(0)=i et y'(0)=0.

Attention aussi, il me semble que la résolution des équations différentielles lineraires à coefficients constants s'énonce plutôt comme ca:

Soit P le polynôme associé l'équation en question. On peut donc l'écrire:

[TEX] P = (X-a_1)^\alpha_1...(X-a_n)^\alpha_n [\TEX]

La solution s'écrit alors:

[TEX] y = P_1e^a_1 + ... + P_ne^a_n [\TEX] avec [TEX] deg P_i = \alpha_i - 1[\TEX]

Sinon j'imagine que tu voulais savoir comment montrer que Vect(cos(.);sin(.)) = Vect(exp(i.);exp(-i.)) en lien avec lequation differentielle y''+y=0. Ca se fait en passant par les relations liant toutes ces fonctions.

[egan]

J'ai peut être un peu répondu à côté de la plaque. Pour une équation de degrés deux, ça se fait bien en utilisant les relations dont je parlais dans mon post précédent et le fait que les racines sont conjuguées. Je ne suis pas sur en revanche que cela se généralise simplement à tout ordre.

[greghowe]

Merci pour ta réponse

il s'agit en fait d'une équation à coefficients réels constants pour lequelle on a des conditions initiales fixées.
le polynome caractéristique scindé à racine simple(réelles et complexes) dans mon cas permet de déterminer la solution complexe, de sorte que cette solution est combinaison linéaire d'exponentielle de ces racine. les conditions initiales permettent alors de trouver la solution complexe exacte. moi ce que je cherche c'est: connaissant la forme de la solution réelle qui elle aussi est une combinaison linéaire d'exponentielle et de produit d'exponentielle par sin et cos, comment fait on pour passer de la solution complexe à la solution réelle ou plus simplement comment retrouver les coefficients de la solution réelle à partir de ceux de la solution complexe?

[greghowe]

c'est un truc en méca donc c'est pour ça que je m'intéresse au solutions réelles...

[JeanJ]

Merci pour ta réponse

il s'agit en fait d'une équation à coefficients réels constants pour lequelle on a des conditions initiales fixées.
le polynome caractéristique scindé à racine simple(réelles et complexes) dans mon cas permet de déterminer la solution complexe, de sorte que cette solution est combinaison linéaire d'exponentielle de ces racine. les conditions initiales permettent alors de trouver la solution complexe exacte. moi ce que je cherche c'est: connaissant la forme de la solution réelle qui elle aussi est une combinaison linéaire d'exponentielle et de produit d'exponentielle par sin et cos, comment fait on pour passer de la solution complexe à la solution réelle ou plus simplement comment retrouver les coefficients de la solution réelle à partir de ceux de la solution complexe?

Avec une EDO a coefficients réels, les solutions sont des combinaisons linéaires de fonctions réelles et/ou de fonctions complexes et leurs complexes conjugués respectifs.
Il suffit donc de séparer d'une part la partie réelle, d'autre part la partie imaginaire, de chaque fonction complexe, puis de les ajouter, ou de les soustraires deux à deux.
Autrement dit : Si f(x) est une solution complexe, on met sous la forme f(x) = A(x) +i*B(x) avec A(x) et B(x) réels.
Forcément g(x)=A(x)-i*B(x) est aussi solution.
La somme des deux est solution : f(x)+g(x) = 2 A(x). Donc A(x) est une solution réelle.
La différence, multipliée par i est solution : i*(g(x)-f(x)) = 2 B(x). Donc B(x) est solution.

Par exemple, si exp(ix) est solution, alors forcément exp(-ix) est aussi solution. La somme des deux est réelle : 2cos(x). Donc cos(x) est solution . La différence multipliée par i donne 2sin(x). Donc sin(x) est solution.

[greghowe]

je pense que ma question n'est pas très clair, je la reformule:


Quelle est la relation entre les coefficients de la solution réelle vérifiant les conditions initiales et ceux de la solution complexe vérifiant aussi ces conditions.
Dans notre cas et d'après Cauchy Lipschitz ces solutions sont uniques et donc les coefficients aussi. mais comment passer de la solution complexe à la solution réelle c'est ça mon problème.

[egan]

Prennons l'exemple de l'équa. diff. y'' + y = 0.
Tu sais que les solutions sont de la forme:



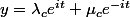
A conditions initiales fixées,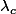 et 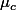sont fixés. Je les considère donc désormais fixés.
Mais on peut aussi écrire, avec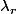 et 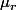fixés,



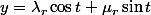
Je pense tu sais que:



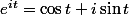
On en déduit que:



Il est temps de mettre en évidence une propriété de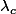 et .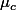
On sait que y est une solution réelle donc y est égale à son conjugué:



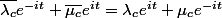
Or les fonctions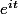 et 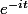forment une famille libre donc:



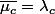
Les coefficients complexes sont donc conjugués si la solution est réelle !

On finit donc par récupérer:



Les fonctions cos et sin formant une famille libre, on termine avec:





J'espère qu'il n'y a pas de faute de signe ou de grosse bêtise dans ce que j'ai raconté mais avec ça, je pense que tu comprends l'idée. Je te laisse le soin de généraliser...

[JeanJ]

je pense que ma question n'est pas très clair, je la reformule:


Quelle est la relation entre les coefficients de la solution réelle vérifiant les conditions initiales et ceux de la solution complexe vérifiant aussi ces conditions.
Dans notre cas et d'après Cauchy Lipschitz ces solutions sont uniques et donc les coefficients aussi. mais comment passer de la solution complexe à la solution réelle c'est ça mon problème.

Tu as donc la solution unique (compte-tenu des conditions données) et tu dis que cette formule contient des fonctions complexes.
On te l'a déjà dit : Tu sépares chaque fonction complexe en sa partie réelle d'une part et imaginaire d'autre part. Il n'y a pas à changer les coefficients. Après cette opération, la formule en question se simplifie et il ne reste que du réel. Un point c'est tout.
Bien sûr, ceci n'est vrai que si les coefficients (de l'équation différentielle donnée au départ) sont réels.
Suppose que ce ne soit pas vrai et qu'il reste un terme imaginaire dans la solution, après la simplification. Alors, le conjugé de cette solution serait aussi solution. On aurait deux solutions différentes, ce qui est absurde, puisque la solution est unique.