Faux pendule.

[Black Jack]

Bonjour,

J'ai trouvé, sur un autre site, un exercice qui paraît simple au premier abord, mais ...



Soit la situation du dessin, on lache le trombone sans lui donner de vitesse initiale.

Ma question (qui n'était pas celle de l'exercice proposé) :

Quelle est l'équation de la trajectoire du trombone ?

Seule la partie de la trajectoire "1er faux quart de tour" m'intéresse.

Pour fixer les idées, soit R la distance entre le trombone et le bois horizontal en t = 0, m la masse du trombone et M la masse qui descend (avec M > > m)

:zen:

[Benjamin]

Salut,

Est-ce qu'on doit considérer des frottements entre la ficelle et la tige ?

[Black Jack]

Salut,

Est-ce qu'on doit considérer des frottements entre la ficelle et la tige ?

Salut,

On peut les "oublier" du moins dans un premier temps ou on peut les incorporer dans les calculs quitte à les faire tendre vers 0 dans les équations trouvées.

Je suis curieux des réponses à venir, car je ne pense pas que ce soit immédiat, je ne suis d'ailleurs pas sûr du tout de la bonne tactique à tenir pour y arriver. J'ai fait quelques approches mais ne suis satisfait d'aucune.

Ce machin semble simpliste, mais ce n'est probablement pas le cas.

:zen:

[Benjamin]

J'ai pas le temps tout de suite, mais je pense qu'avec le théorème de l'énergie cinétique, ça se passera pas trop mal. Simple intuition.

[Kikoo <3 Bieber]

Salut vous deux !

Alors moi je suis sur les courbes paramétrées en maths et sur de la dynamique classique en physique. Je suis super intéressé par ce problème (tant sur le plan divertissement qu'au niveau de mes études), et donc je me demande s'il est abordable par un petit hypotaupe :)

PS : et pis j'ai colle de physique demain, ce sujet tombe à pic !

[Mathusalem]

Est-ce que l'on considère le point tige-corde comme fixe dans l'espace ?

C'est-à-dire est-ce que le problème à résoudre est celui d'un pendule le longueur variable, longueur qui varie comme L(t) = L_0 + 1/2gt^2 ?

[Black Jack]

Est-ce que l'on considère le point tige-corde comme fixe dans l'espace ?

C'est-à-dire est-ce que le problème à résoudre est celui d'un pendule le longueur variable, longueur qui varie comme L(t) = L_0 + 1/2gt^2 ?

Tu peux faire comme tu veux ... pourvu qu'au final les conclusions soient bien celles qui correspondent à l'expérience.

Mais méfie-toi de ne pas aller trop vite, certes, en première approximation, on a bien L(t) = L_0 - 1/2gt^2, mais les résultats auxquels on arrive en partant de cette approximation ne semblent pas (sauf erreur de ma part) conformes à l'expérience (c'est à dire aux résultats des essais concrets).

:zen:

[Mathusalem]

Tu peux faire comme tu veux ... pourvu qu'au final les conclusions soient bien celles qui correspondent à l'expérience.

Mais méfie-toi de ne pas aller trop vite, certes, en première approximation, on a bien L(t) = L_0 - 1/2gt^2, mais les résultats auxquels on arrive en partant de cette approximation ne semblent pas (sauf erreur de ma part) conformes à l'expérience (c'est à dire aux résultats des essais concrets).

:zen:

Je crois pas que la longueur diminue au cours du temps, si ?

EDIT: Ah mal compris, je croyais qu'on voulait la trajectoire du pendule vertical.

[Benjamin]

Salut,

Si on considère que M >> m, je suis d'accord avec Mathusalem qu'a priori, on peut dire que r=R-1/2gt².

Ca nous donne r' = -gt et ainsi l'équation différentielle pour le trombone :

, avec résolution numérique obligatoire.

Si tu ne trouves pas la même chose, quelques pistes qui me viennent :
- Problème d'intégration numérique de l'équa diff donnée
- Les frottements corde / tige sont trop importants pour être négligés
- La ficelle n'est pas inextensible, ce qui fait foirer r=R-1/2gt²
- Il y a une erreur dans le raisonnement m r=R-1/2gt² (si on suppose pas de frottement et ficelle inextensible).

[Black Jack]

Salut,

Si on considère que M >> m, je suis d'accord avec Mathusalem qu'a priori, on peut dire que r=R-1/2gt².

Ca nous donne r' = -gt et ainsi l'équation différentielle pour le trombone :

, avec résolution numérique obligatoire.

Si tu ne trouves pas la même chose, quelques pistes qui me viennent :
- Problème d'intégration numérique de l'équa diff donnée
- Les frottements corde / tige sont trop importants pour être négligés
- La ficelle n'est pas inextensible, ce qui fait foirer r=R-1/2gt²
- Il y a une erreur dans le raisonnement m r=R-1/2gt² (si on suppose pas de frottement et ficelle inextensible).

Si on considère que M >> m, je suis d'accord avec Mathusalem qu'a priori, on peut dire que r=R-1/2gt²

Oui, reste quand même à voir ce qu'on entend par M > > m car je désire rester pas trop loin d'essais pratiques facilement réalisables.

Le "pendule" retient un peu la masse qui descent via la ficelle, par une composante de son poids variant avec theta et avec la force centrifuge sur le trombone ... reste à estimer si le "un peu" ne doit pas être pris en compte dans des essais pratiques, donc avec évidemment M > > m mais pas M > > > > m

Sauf erreur de ma part, en partant de ton équation (avec R = 1 m), je trouve que en theta = 0 (ficelle verticale), on a w = 21,8 rad/s en t = 0,366 s et r = 0,343 m

--> w²r = 163 (SI)

et donc par exemple si M = 50 m, on aurait : mw²r/Mg = 163/(50*9,81) = 0,33

Et l'effort centrifuge exercé par le trombone via la ficelle sur la masse qui descend n'est pas négligeable, du moins vers la fin du 1er "faux" 1/4 de tour.

Mais si évidemment, on a un rapport des masses qui est très très trés grand, alors on peut oublier cette influence.
J'ai essayé d'en tenir compte et donc mes équations sont plus compliquées ... elles contiennent m et M, que je peux faire varier facilement dans les résolutions numériques.

Il faudrait que j'essaie de les revoir ... si je m'y retrouve dans mes notes écrites un peu n'importe comment.

:zen:

[Benjamin]

Re,

Une autre idée m'est venue : on fait l'hypothèse que la fil est sans masse, ce qui est traduit en réalité par m_fil << m_trombone.

Quand je vois la masse d'un trombone, je me demande si on a pas un pendule avec en réalité une masse distribuée sur toute la longueur.

Pour l'AN, avec R=1m, je trouve la même chose que toi (sauf que chez moi, j'ai pris la convention de signe qui fait que w est négatif).

[Black Jack]

Re,

Une autre idée m'est venue : on fait l'hypothèse que la fil est sans masse, ce qui est traduit en réalité par m_fil << m_trombone.

Quand je vois la masse d'un trombone, je me demande si on a pas un pendule avec en réalité une masse distribuée sur toute la longueur.

Pour l'AN, avec R=1m, je trouve la même chose que toi (sauf que chez moi, j'ai pris la convention de signe qui fait que w est négatif).

J'ai fait des essais avec M = 40 g et m = 0,9 g (ce n'était pas un trombone, mais soit)
Je viens de chercher la masse linéique du fil (on trouve vraiment de tout sur le net) et c'est environ 30g/1000m, soit donc masse du fil (1m) = 0,03 g

Les résultats étaient presque identiques avec des tiges horizontales avec un diamètre allant de 3 à 10 mm, ces "tiges" étaient lisses (sans aspérités et glissantes au toucher).

Résultats trouvés : environ 20 cm de fil s'enroulent sur la tige ... ce qui montre bien que la masse qui descend a communiqué de l'énergie au trombone ...

Ce n'est pas trop loin des 34 cm trouvés avec ta formule qui ne tient pas compte des effets mentionnés (comme la force centrifuge du trombone qui via la ficelle freine la masse qui descent (et donc modifie le dr/dt). Mes calculs, en tenant compte du rapport des masses donnaient des distances très petites (1 ou 2 cm). Il faudra vraiment que j'essaie de débrouiller mes notes, j'ai du faire une erreur quelque part, les équations en tenant compte du rapport M/m (et de la force centrifuge et de la composante du poids de m ralentissant M) sont évidemment plus complexes ... et il est bien probable que je me sois planté quelque part.

Ou bien comme tu le dis, cela vient de ce qui a été négligé ou mal "senti" comme la masse du fil ou les frottements ou ...

:zen:

[Mathusalem]

Qu'est-ce que tu entends par le fil qui s'enroule ?

Moi j'ai un couple d'équations différentielles non linéaires couplées pour l'horizontale et la verticale.

La supposition d/dt r(t) = - gt est bel et bien vérifiée pour m_trombone << m_masse. Il suffit de résoudre le problème de machine d'Atwood avec une des masses qui est inclinée pour s'en convaincre.

J'ai pas inclu l'inertie de la barre et pour l'instant dans mon équa diff j'ai pas considéré m_trombone << m_masse. J'essayerai de regarder la solution numérique ce soir, mais c'est quoi le paramètre que tu peux tester ?

[Benjamin]

Re,

tu as raison BJ, il manque la force centrifuge du trombone, qui ne peut pas se simplifier à priori !! Sauf à supposer que m --> 0 mais c'est moche.

Le couple d'équations différentielles est donc (attention, on a quand même m << M ici) :
et



Ceci dit, dans le cas présent ça change rien en fait.

Avec m = 0
t=0.3658s et r=34.3755mm

avec m = 0.9g et M = 40g
t=0.3668s et r=34.8242mm

[Black Jack]

Qu'est-ce que tu entends par le fil qui s'enroule ?

Moi j'ai un couple d'équations différentielles non linéaires couplées pour l'horizontale et la verticale.

La supposition d/dt r(t) = - gt est bel et bien vérifiée pour m_trombone << m_masse. Il suffit de résoudre le problème de machine d'Atwood avec une des masses qui est inclinée pour s'en convaincre.

J'ai pas inclu l'inertie de la barre et pour l'instant dans mon équa diff j'ai pas considéré m_trombone << m_masse. J'essayerai de regarder la solution numérique ce soir, mais c'est quoi le paramètre que tu peux tester ?

Mon test n'est pas des plus "précis", mais soit.
Je peux tester "l'altitude" du trombone lorsqu'il passe pour la première fois dans le plan vertical passant par le bois horizontal ...
Et je peux mesurer aussi la longueur de ficelle qui s'enroule autour du bois, mais là, je me méfie de la mesure à cause du glissement du fil sur le bois même après que la première boucle ne soit refermée sur elle-même et bloque violemment la masse qui descend.

:zen:

[Black Jack]

Re,

tu as raison BJ, il manque la force centrifuge du trombone, qui ne peut pas se simplifier à priori !! Sauf à supposer que m --> 0 mais c'est moche.

Le couple d'équations différentielles est donc (attention, on a quand même m << M ici) :
et



Ceci dit, dans le cas présent ça change rien en fait.

Avec m = 0
t=0.3658s et r=34.3755mm

avec m = 0.9g et M = 40g
t=0.3668 et r=34.8242mm

C'est très possible car la force centrifuge sur la masse m ne prend des valeurs non négligeables devant le poids de la masse M que vers la fin du 1er faux "quart de tour".

:zen:

[Mathusalem]

Je regarderai ce soir avec mon équa-diff non simplifiée. Benjamin : tu as utilisé un schéma de différences finies ?

[Benjamin]

J'ai utilisé la fonction ode23 de Matlab, sans option supplémentaire : ode23 is an implementation of an explicit Runge-Kutta (2,3) pair of Bogacki and Shampine. It may be more efficient than ode45 at crude tolerances and in the presence of moderate stiffness. Like ode45, ode23 is a one-step solver.

[Mathusalem]

J'ai pas encore testé numériquement mon équation différentielle, mais pour être sûr qu'on est sur la même longueur d'onde, et qu'on considère le même problème, voici mon développement pour arriver à l'équa-diff.

Je considère le système avec l'axe z vertical vers le bas, je fixe arbitrairement la position initiale z=0. L'angle entre l'horizontale et le fil est . Je fixe la direction x horizontale positive dans la direction du mouvement et x=0 la position initiale.

On appelle la masse du trombone, et la masse du poids. La gravité et la tension du fil sont les forces à considérer.

On peut calculer la norme de la tension du fil



En projetant sur l'axe vertical et horizontal la 2nde loi de Newton appliquée au trombone, on obtient




Cependant, géométriquement,
Et on a les relations



Et en posant on obtient



et



Jusque là il me semble que le problème est exact sans les considérations de friction. Je regarderai plus tard pour implémenter la résolution de ce couple d'équations avec matlab. Est-ce que l'on est d'accord? Noter aussi que j'ai pas de dérivée première dans mon expression, mais bon je pense que ça provient du changement de variable (x,z) -> (r,theta)

[Benjamin]

Salut,

je n'ai pas du tout procédé comme toi. Déjà pour un problème de rotation, je n'aime pas utiliser x et z. Je travaille en R et theta.

J'oriente x vers le bas, y vers la droite. Mon angle theta est défini à partir de x=0 en le comptant positif de x vers y. A t=0, theta=90°.

J'ai 2 corps : la masse et le trombone. J'ai donc 2 grandeurs associées à chacun : r_m, theta_m, r_t, theta_t.

La seule force qui apporte un couple est le poids. Le moment du poids par rapport à l'axe est r^P = -r*m*g*sin(theta)e_r^e_theta=-r*m*g*sin(theta)e_z.

Par ailleurs, le moment cinétique du pendule par rapport à l'axe est m*r^v. On sait que l'expression générale de la vitesse dans la base cylindrique est v=(r')e_r+(r*theta')e_theta donc le moment cinétique vaut m*r²*theta'e_z.

En appliquant le théorème du moment cinétique en l'axe du pendule, on a que la dérivée temporelle du moment cinétique égale la somme des moments extérieurs.

La dérivée de m*r²*theta', c'est m*(2*r'*r*theta'+r²*theta").
On a donc m*(2*r'*r*theta'+r²*theta") = -r*m*g*sin(theta) ce qui conduit à

theta"+ 2*r'*theta'/r + g/r*sin(theta)=0

Cette formule est générale à tout pendule où il n'y a que le poids qui agit en plus de la tension du fil. On voit que si r'=0, ficelle de longueur donnée, on retrouve l'équation classique et bien connue theta" + g/r*sin(theta)=0.

On a donc 2 premières équations.




On sait que theta_m à t=0+ égale 0 donc theta_m=0 pour tout t (ce qui est confirmé par l'équation différentielle 1) ==> Logique aucun moment ne s'applique qui puisse mettre en rotation la masse (avec la modélisation "parfaite" qu'on en fait).
Il reste donc


Ensuite, j'applique le PFD à la masse et au trombone dans R galiléen mais projeté sur e_r_m et e_r_t. En appelant T la tension dans la fil (compté positif), il vient
Pour la masse (on sait que theta = cte) :


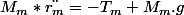
Pour le trombone (dans le cas général, l'accélération centripète va r"-r*(theta')² :


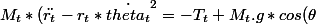La ficelle est parfaite, donc T_t=T_m=T et r_t"=-r_m".

On aboutit donc aux 3 équations suivantes :




.

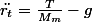
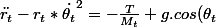3 équations ; 3 inconnues : T, r_t et theta_t.

La suite après.