Cardinal quantitatif et autres travaux mathématiques (1)

[Ben314]

Comment diable veut tu que je lise ou juge la suite vu que l'ensemble sur lesquels tu as l'air de vouloir travailler on sait pas ce que c'est".
Tu pense vraiment qu'on peut répondre a une question du style "est-elle rouge ?" sans savoir ce que désigne le "elle" de la phrase. Moi, je sais pas répondre tant qu'on m'a pas dit qui était le "elle" en question, désolé.

[Ben314]

Cet ensemble bien que mal formalisé, est clairement intuitif.

Et bien, tu reviendra en parler quand il sera formalisé, et là, tu pourra éventuellement faire des math avec, mais les mot "intuitif" et "mathématique", on sait depuis plus d'un siècle que ça ne fait vraiment pas bon ménage.

[bolza]

Bonjour, je n'ai pas vu qu'il y a vait ce fil.

J'ai décidé d'y intervenir parce qu'il y a quelque chose qui me déplaît dans ce que vous dites :

J'ai eu un mal fou à exprimer mes intuitions, plus tard confirmées par Michel Coste (professeur à l'Université RENNES 1) et Denis Feldmann (professeur en classe préparatoire et contributeur à Wikipedia), dans la littérature (d'où le "Mon" inapproprié), dans ZFC, mais dans un contexte bien précis.

Que vous vous amusiez à définir un concept flou que vous essayer vainement de formaliser, si vous voulez,
mais que vous utilisiez le nom de quelqu'un d'autre (ici Michel Coste ou Denis Feldmann)
pour vous donnez de la crédibilité, là je ne suis pas d'accord.

Si pour Michel Coste vous faite référence au pdf que vous avez donnez sur l'autre fil,
je vous ai déjà dit ce que j'en pense. Et ne me dite pas que c'est un article de vulgarisation,
car même un article de vulgarisation reste un article. Et il se trouve que dans cet "article",
on retrouve les même "fautes de gouts" qui sont dans vos pdf et signaler par Ben314,
fautes de gout qu'aucun chercheur ne fait (sinon il n'a aucune chance d'être publier).

De plus même dans les articles de vulgarisation, (et je dirait même surtout dans les articles de
vulgarisations) il y a des références précises vers des travaux publiés

Vous affirmer que vos intuitions on été plus tard "confirmer" dans la littérature.
De quel littérature parlez vous ? Si c'est vraiment le cas alors veuillez donner des références
préçises de papier publié en préçisant la date de publication, l'endroit où cela a été publié, etc.

Avez-vous lu au moins déjà un article dans votre vie ??
si c'était le cas vous sauriez au moins comment ça se présente.

Donc à part une référence préçise de votre part, arretez de vous cachez derrière des noms
de chercheurs en espérant que cela vous apporte du crédit, car pour l'instant, ça fait plutôt
l'effet inverse.

EDIT : Je connais maintenant le contexte dans lequel ce papier a été écrit, et qui expliquent
certains "vice de forme" qui me faisait douté que ce soit lui qui l'ai écrit.
Mais sachez que quand on parle de "la littérature" à propos de travaux scientifiques, on fait
référence à des papiers publié, ce papier ne fait pas parti de la "littérature" au sens où on l'entend habituellement, il a été poster sur un forum mathématiques, mais il n'a pas été publié.
Faites attention à cela, si vous parler de "la littérature", c'est que vous êtes capable de donner des références préçise vers un papiers publié.

[bolza]

Un mathématicien peut modifier, rectifier, corriger son intuition, au cours de ses expériences, et même si celle-ci ne correspond plus à l'intuition commune, il en aura toujours besoin.

Enfin une phrase sensé de votre part...
Le problème c'est que vous au lieu de modifier, rectifier, corriger son intuition, au cours de vos expériences,
vous voulez modifier, rectifier, corriger la théorie pour qu'elle correspondent à votre intuition.
Je vous ai dit que ce n'est pas comme ça qu'on fait des math, ou même des sciences en général,
En science on modifie, rectifie, corrige une théorie pour qu'elle correspondent à des expériences,
pas à des "intuitions".

[beagle]

Les mathématiques ont un statut, à part, et n'ont pas besoin de coller à la réalité.

c'est vrai, néanmoins la phrase de bolza pourrait se comprendre aussi, comme :
dans quelles situations de problème mathématique (remplaçant ici le mot expérience ) aurait-on un intérèt quelconque à utiliser tes nouveaux outils versus les anciens qui seraient moins performants.

alors tu peux toujours dire , on verra ensuite à quoi cela sert.Ok.
reste à te coltiner de construire un truc cohérent.
Or il t'est reproché de mal définir tes points de départ il me semble,
donc cela empèche la possibilité de lire un développement quelconque.

Voilà ce que je comprends de tes dialogues avec les matheux du site comme Ben314 et bolza ...

Perso sur le peu que je comprenais de ce que tu voulais faire, ben je trouvais cela intéressant ...

[Guillaume De Normandie]

message supprimé

[beagle]

Va maintenant jeter un coup d'œil sur mon message de 17h53, de l'autre fil.

Je suivais ce fil avec intérèt bien que n'ayant pas les connaissances requises pour te comprendre ou pour comprendre les réponses qui te sont apportées.
Je n'étais qu'à un niveau intuitif de ce que tu essayes de faire.

Malheureusement la police de la pensée a encore frappé et son verdict est irrévocable, fin du fil de discussion.
On se fiche royalement des gens intéressés qui suivaient le fil.Ce fil est susceptible de géner certains lecteurs, cela suffit à justifier sa fermeture.

[beagle]

Tu peux continuer à le suivre, sur ce fil, à partir du message précédent.

je ne m'en prive pas.

je mets la ref Villani sur l'erreur car j'avais tout à fait cela en tète lorsque l'on ferme des fils de discussions pour empécher que des fils plein d'erreurs ne viennent polluer le site.Cela pose effectivement le problème de laissez donc les gens se gourrer, laissez nous apprendre des erreurs des autres.J'ai beaucoup appris de fil de discussion full error.:
Cédric Villani:"Difficile de les hiérarchiser. Il y a, en tous cas, une vraie différence de culture entre les approches anglo-saxonne et française.

Dans la première, par exemple, l’erreur est vue comme la marque d’un contact avec la réalité, et donc comme une expérience. C’est comme ça qu’on apprend. Cela peut même être valorisant ! Dans le système américain, les gens vont même se targuer de leurs erreurs. Mais c’est pour mieux montrer la persévérance grâce à laquelle ils les ont surmontées. Réussir après de nombreux échecs donne encore plus de prestige à la réussite !

Dans une vision plus française, disons cartésienne, on considère que les choses sont écrites depuis le départ. Soit la méthode est bonne et elle ne connaîtra que des réussites. Soit elle est mauvaise et n’aboutira qu’à des erreurs. L’erreur est même considérée comme une vraie faute (pensez à l’expression française « faute d’orthographe ») !

C’est le système français qui a un problème avec l’erreur. Et il est difficile de faire admettre qu’elle est la base de toute démarche scientifique, de tout raisonnement."

Maintenant je ne te cache pas que je suis assez fan de Ben314, et lorsque Ben314 dit qu'il ya soucis, c'est qu'il ya soucis, et c'est donc bien le moment de le reconnaitre, de voir où et pourquoi.
Mais il me semble aussi que ta démarche essaye également d'avncer et de corriger,
donc perso je n'ai pas compris que l'on ferme le fil.
Alors si celui-ci continue je vais continuer à te lire.
Mais je ne te cache pas que ce n'est pas de mon niveau ...
Bonne continuation...

PS: c'est bien pour cette raison que je parle de police de la pensée,
mot bien fort pour ce site et l'intervention de Benjamin, qu'il m'en excuse, il connnait mes exagérations de langae également.Mais dans la société française dans tous les domaines, politiques, philosophiques, on assiste depuis ces dernières décennies à une vraie police de la pensée avec un totalitarisme qui nie en le diabolisant les pensées adverses et qui ne combat pas avec des arguments mais avec des condamnations morales, ceux qui pensent bien (qui sont dnas le vrai,comme eux) et ceux qui pensent mal (qui sont dans l'erreur), qui sont le mal (alors qu'il ne s'agit que d'une pensée différente ou adverse).
Quand bien mème les gens penseraient ce qu'ils pensent, foutez leur la paix au nom du dorit à penser différent et mème du droit à penser en faisant des erreurs ...

[beagle]

A part des connaissances élémentaires, en théorie des ensembles, ainsi, qu'en théorie de la mesure, appliquées à l'ensemble des parties de , voire sur la notion de bijection, ma notion de cardinal quantitatif ne demande pas beaucoup de connaissances.

Mon avant-dernier message avant celui-ci, ne nécessite ni théorie de la mesure, ni de notion de bijection.

jamais bossé les parties de R, si c'est simple je pourrais pte comprendre,
mais la curiosité qui était la mienne c'est aussi que signifie l'inclusion dans les ensembles infinis,
quels sens et quelles gourrances possibles pour quiqui connait rien = moi!

exemple:
quand il y en a le double il y en a autant:
il ya autant de rayons du demi-cercle que de diamètre du cercle,
donc bijection de 1 diamètre vers deux rayons, c'est comme si double

oui, sauf qu'il y aussi bijection de 1 diamètre vers 1 rayon = le autant

donc en matière d'inclusion, t'es sur qu'on n'a pas des soucis????

[bolza]

Matheux Philosophe, dans votre message précédent lisez le message que vous avez mis en citation,
et lisez ce que vous avez écrit en dessous et dites moi s'il vous plaît quel est le rapport entre les 2 ??

En faite non ne me le dites pas, ce n'est pas pour ça que j'interviens ici.
Je veux d'abord m'excuser pour avoir douter de vos propos à propos du pdf de Michel Coste,
C'est bon, maintenant je sais dans quel contexte ce pdf a été écrit (voir l'EDIT du message à ce sujet
plus haut).

Ensuite (oui parce que cette histoire me trotte dans la tête quand même) Il y a quelques paradoxes
et question que je voudrais que vous m'expliquiez.

Mais d'abord, je voudrais que vous répondiez à mes questions par oui, ou par non
(en apportant quelques préçisions si vous voulez) , mais surtout sans faire comme dans le message précédent,
un copier/coller des propriétés de votre cardinal (car ça ne répond à rien), merci.


1)-Donc si j'ai bien compris vous voulez un cardinal tel que deux figures superposables
aient le même nombre d'élément ?

2)-Et donc votre cardinal doit être invariant :
a) par translation ?
b) par rotation ?

[bolza]

jamais bossé les parties de R, si c'est simple je pourrais pte comprendre,
mais la curiosité qui était la mienne c'est aussi que signifie l'inclusion dans les ensembles infinis,
quels sens et quelles gourrances possibles pour quiqui connait rien = moi!

exemple:
quand il y en a le double il y en a autant:
il ya autant de rayons du demi-cercle que de diamètre du cercle,
donc bijection de 1 diamètre vers deux rayons, c'est comme si double

oui, sauf qu'il y aussi bijection de 1 diamètre vers 1 rayon = le autant

donc en matière d'inclusion, t'es sur qu'on n'a pas des soucis????

Attention, une bijection 1 vers 2 ça n'existe pas !!
1 vers un couple si vous voulez, mais pas 1 vers 2 !!!
ça peut paraître joué sur les mots mais non, car sinon votre bijecion n'est même pas une fonction.
Pour un x fixer, une fonction f ne peut avoir qu'une seul valeur pour f(x) pas deux.
Et il faut faire attention avec le nombre de couple. par exemple dans les couples
(a,b) (a,c) (b,a) (a,a) on a quatre couple différent, mais que trois éléments (pas 8).
donc il faut vérifiez certaines conditions avant de passer au "*2".

[beagle]

Attention, une bijection 1 vers 2 ça n'existe pas !!
1 vers un couple si vous voulez, mais pas 1 vers 2 !!!
ça peut paraître joué sur les mots mais non, car sinon votre bijecion n'est même pas une fonction.
Pour un x fixer, une fonction f ne peut avoir qu'une seul valeur pour f(x) pas deux.
Et il faut faire attention avec le nombre de couple. par exemple dans les couples
(a,b) (a,c) (b,a) (a,a) on a quatre couple différent, mais que trois éléments (pas 8).
donc il faut vérifiez certaines conditions avant de passer au "*2".

non, il s'agit de 1 vers 2 différents donc pas (a,a) et cela n'est pas orienté au sens que (a,b) = (b,a),
mais c'est orienté au sens que je peux dire où est a ou bien b
prenons in exemple tout bète:
un homme: pour une tète j'ai deux bras alors c'est orienté car bras gauche ou bras droit je sais le définir mais je ne dis pas une tète c'est (bras G , bras D) ainsi que bras D , bras G)
Bref pour les rayons c'est simple, un cercle peut se couper en deux morceaux par un diamètre, j'ai un demi-cercle supérieur et un demi-cercle inférieur par exemple.
Bien, alors le une tète deux bras, ici c'est
pour un diamètre donné quelconque, j'ai deux rayons, un dans chaque demi-cercle.
c'est vrai pour touit diamètre, pour un diamètre donné j'ai deux rayons et deux seuls,
idem pour un rayon donné j'ai un diamètre et un seul.
Bref si cela ne dit pas que j'ai le double de rayons par rapport aux diamètres, je ne sais pas ce qu'il faut dire.

Maintenant on démontre AUSSI = EGALEMENT qu'il existe une bijection qui a un diamètre associe un seul rayon, tous les diamtres du cercles en bijections avec tous les rayons du cercle.
Ceci se traduit par il y a autant de rayons que de diamètre.

Il me semble que c'est un exemple du fait que deux fois le mème infini c'est l'infini de départ en terme de cardinalité des infinis de Cantor.

Et perso j'ai du mal à le traduire mais en terme d'inclusion tout se passe comme si l'ensemble des rayons du cercle pouvait s'inclure dans l'ensemble des rayons du demi-cercle, ce qui gène un peu la compréhensionde l'inclusion, enfin l'intuition que je m'en fais,
voili , voilo

[bolza]

@Matheux philosophe :

3)-Est-ce que les réponse à ces questions sont les mêmes si les ensembles en question sont discrets ?
(par discret j'entends dénombrable i.e du même ordre de grandeur que N selon vous)

4)- là ou je veux en venir c'est dans l'exemple suivant :



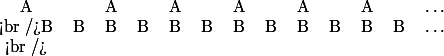
(les trois petit points signifies que le schéma se répète à l'infini)

Selon votre cardinal, il y a -t-il "2 fois plus" de que de ?

P.S. :Je sais pas comment intégrer un dessin, alors je fais avec les moyen du bord ,
en fait les A sont des points alignés et le B aussi.
Quand un A ets audessus d'un B c'est que les points sont l'un au dessus de l'autre.

[beagle]

@Matheux philosophe :

3)-Est-ce que les réponse à ces questions sont les mêmes si les ensembles en question sont discrets ?
(par discret j'entends dénombrable i.e du même ordre de grandeur que N selon vous)

4)- là ou je veux en venir c'est dans l'exemple suivant :



(les trois petit points signifies que le schéma se répète à l'infini)

Selon votre cardinal, il y a -t-il "2 fois plus" de que de ?

P.S. :Je sais pas comment intégrer un dessin, alors je fais avec les moyen du bord ,
en fait les A sont des points alignés et le B aussi.
Quand un A ets audessus d'un B c'est que les points sont l'un au dessus de l'autre.

pour moi,oui, on peut dire double de B que de A,
c'est idem à double des impairs pour les entiers.

et tu vas démontrer qu'il y en AUSSI = EGALAMENT le mème nombre, c'est ça?
c'est bien parce qu'il y en a autant quand il y en a le double.

d'où l'idée de passer par l'inclusion, mais l'inclusion marche-t-elle sans incohérences?

[bolza]

Bref si cela ne dit pas que j'ai le double de rayons par rapport aux diamètres, je ne sais pas ce qu'il faut dire.

Là est justement la question beagle ça veut dire quoi le double ?
La notion de double pour moi est défini sur les nombres :
Je prend 5, le double de 5 c'est 10 ok.

Mais là on ne parle pas de nombre, on parle d'infini.
Alors le double de l'infini c'est quoi ? quels sens cela à-t- il ?

Si on dit que si on double une quantité infini alors on a toujours une quantité infini,
Alors on revient à comparer l'infini issu du double de l'infini avec l'infini de départ.

Et donc on en reviens à la première question comment comparer deux infini ?
Dans le cadre classique actuelle (où on utilise les bijections), on s'aperçoit que ici que "doublé un infini ne le change pas"
et donc la notion de "double" sur un infini (si tenté qu'elle ait un sens) n'est pas du tout la même
(en tout cas n'a pas du tout les même propriétés) que la notion de double sur les nombres finis.

[beagle]

Là est justement la question beagle ça veut dire quoi le double ?
La notion de double pour moi est défini sur les nombres :
Je prend 5, le double de 5 c'est 10 ok.

Mais là on ne parle pas de nombre, on parle d'infini.
Alors le double de l'infini c'est quoi ? quels sens cela à-t- il ?

Si on dit que si on double une quantité infini alors on a toujours une quantité infini,
Alors on revient à comparer l'infini issu du double de l'infini avec l'infini de départ.

Et donc on en reviens à la première question comment comparer deux infini ?
Dans le cadre classique actuelle (où on utilise les bijections), on s'aperçoit que ici que "doublé un infini ne le change pas"
et donc la notion de "double" sur un infini (si tenté qu'elle ait un sens) n'est pas du tout la même
(en tout cas n'a pas du tout les même propriétés) que la notion de double sur les nombres finis.

Ben il n' y a pas de raison de dire du mal des doubles par rapport aux autant.
J'ai une correspondance de terme à terme, de 1 terme à 1 terme, c'est la bijection classique, c'est le autant,
lorsque j'ai une correspondance de 1 terme à deux termes, tels que tous sont représentés, et que cette correspondance est unique, ben je ne vois rien qui s'oppose à dire que cela définit le double.

Maintenant l'idée de l'inclusion si elle marche , était de dire, ok c'est le mème infini, le mème cardinal, mais si un ensemble était inclus dans l'autre, ben on lui accorderait une quantité moindre.
J'aurais attendu des explications plus convaincantes des tenants de l'orthodoxie sur des exemples de bordel qui en résulterait plutot que de dire à répétition que c'est autant car bijection.Ok, cela me convient autant par bijection, mais est-ce fini là?

[bolza]

Oui, et je suppose qu'après vous allez décaler les , d'un cran vers la droite.

Cf. le lien suivant à partir de la fin de page 4 et aussi de la fin de la page 6 :

http://www.fichier-pdf.fr/2014/12/22/cardinal-quantitatif-de-parties-de-r-n-5/cardinal-quantitatif-de-parties-de-r-n-5.pdf

Non, je ne vais pas décaler les A vers la droite.

5-) Donc en remplacant les A et les B par des nombres (les points restent au même endroit), comme ceci :



On peut en déduire ainsi qu'il y a deux fois plus de nombre pair que de nombre entier c'est bien cela ?

[beagle]

Non, je ne vais pas décaler les A vers la droite.

5-) Donc en remplacant les A et les B par des nombres (les points restent au même endroit), comme ceci :



On peut en déduire ainsi qu'il y a deux fois plus de nombre pair que de nombre entier c'est bien cela ?

OUi, il y a le double,
mais aussi et tu peux le démontrer autant.
Le autant ne nie pas qu'il y en ai le double .

d'où l'idée qui est folle, qui est idiote, qui mène à des incohérences qui je sais pas,
mais d'où l'idée de dire on va classifier AUSSI par inclusion.
Maintenant l'ensemble des entiers s'il est inclu dans l'ensemble des pairs cela va ètre le bordel.
La question est bien pourquoi l'idée de matheuxphilosophe est folle !

[bolza]

Ben il n' y a pas de raison de dire du mal des doubles par rapport aux autant.
J'ai une correspondance de terme à terme, de 1 terme à 1 terme, c'est la bijection classique, c'est le autant,
lorsque j'ai une correspondance de 1 terme à deux termes, tels que tous sont représentés, et que cette correspondance est unique, ben je ne vois rien qui s'oppose à dire que cela définit le double.

D'accord, vous avez donnez un sens a double, ça me va.
Mais ce double là a-t-il les même propriétés que le double sur les nombre ?
car il y en a un qui correspond à une multiplication par deux et l'autre
à une "correspondance entre 1 et 2". Dans le cas fini je vois bien le lien entre les deux.
Mais dans le cas infini ?

Maintenant l'idée de l'inclusion si elle marche , était de dire, ok c'est le mème infini, le mème cardinal, mais si un ensemble était inclus dans l'autre, ben on lui accorderait une quantité moindre.
J'aurais attendu des explications plus convaincantes des tenants de l'orthodoxie sur des exemples de bordel qui en résulterait plutot que de dire à répétition que c'est autant car bijection.Ok, cela me convient autant par bijection, mais est-ce fini là?

Mais c'est bien pour ça que je pose la question : comment compare-t-on deux infini ?
Parceque la seule réponse que je connais pour l'instant c'est il y a une bijection.
Donc je peux vous expliquer des trucs si on est dans ce cadre, mais si on en sort,
c'est à moi qu'il faut expliqué des trucs.

[beagle]

"D'accord, vous avez donnez un sens a double, ça me va.
Mais ce double là a-t-il les même propriétés que le double sur les nombre ?"

je peux vous retourner la question,
deux infinis il y a bijection classique 1 pour 1, = on dit autant de
ce autant de a-t-il les mèmes propriétés que ...

Je n'ai pas à accorder plus de valeur à pour 1 j'ai tiujours 1 et un seul
au pour 1 j'ai toujours 2 deux "uniques"

il se trouve que les deux sont vrais pour N, pour R,
donc pour mes rayons et mes diamètres,...