Vérification d'integrale

par **Eaglenight** » 12 Avr 2007, 10:25

Bonjour à tous , alors voila il y a quelques jours , j'ai poster sur ce forum pour avoir de l'aide au sujet des Integrales pour un Devoir maison . Maintenant , j'ai finis le premier exercice et j'aimerais avoir confirmation des mes réponses .

Voila donc ce que j'ai trouvé :

Intégrale de x=1 à x=2 de 3(3x-5)^7 dx = -255/8 ( sa me parait louche :) )
Intégrale de x=-1 à x=0 de (5x+2)^4 dx = 11
Intégrale de x=-1 à x= 0 de (2t+3)/(t²+3t+3)^4 dt = 26/81
Intégrale de x=0 à x= 1 de x^4/(1+x^5) dx = 3/40
Intégrale de x=0 à x= PI/2 de cos(t)*[sin(t)]^3 dt = 1/4
Intégrale de x= 1/e à x= e de [ln(x)]^5/x dx = 0
Intégrale de x= 1 à x=4 de ((x/2)+RAC(x)-1)^6(1+(1/RAC(x))) dx = 5/24
Intégrale de x= -PI/3 à x= PI/3 de [cos(x)]^3 dx = 3RAC(3)/4

Voila ça fait un peu long à vérifier mais je vous en remerci d'avance .

par **fonfon** » 12 Avr 2007, 10:45

salut,

Intégrale de x=1 à x=2 de 3(3x-5)^7 dx = -255/8 ( sa me parait louche )
Intégrale de x=-1 à x=0 de (5x+2)^4 dx = 11
Intégrale de x=-1 à x= 0 de (2t+3)/(t²+3t+3)^4 dt = 26/81

c'est bon

par **emdro** » 12 Avr 2007, 10:46

Bonjour,

tout est bon sauf:

Intégrale de x=0 à x= 1 de x^4/(1+x^5) dx = 3/40 (j'attends des ln...)

et
Intégrale de x= 1 à x=4 de ((x/2)+RAC(x)-1)^6(1+(1/RAC(x))) dx = 5/24
si j'ai bien lu, cela donne 279935/448.

par **Flodelarab** » 12 Avr 2007, 10:49

fonfon a écrit:salut,

c'est bon

T sur ... car la première, de tête, ça fait 2^16/2^3=2^13 ... pas 2^8 ....
Le 255 me parait louche
mais g ptet fait un faute

par **Flodelarab** » 12 Avr 2007, 10:51

fonfon a écrit:salut,

c'est bon

t sur pour la première ... de tête, je trouve pas ça.

par **fonfon** » 12 Avr 2007, 10:53

Flodelarab a écrit:t sur pour la première ... de tête, je trouve pas ça.

oui, mais j'ai peut-être fais une erreur de calcul car je l'ai fais assez vite je vais reverifier

par **Flodelarab** » 12 Avr 2007, 10:53

non c moi.
Je divisais par 8 et je remettais 1/8 après

par **Eaglenight** » 12 Avr 2007, 10:55

Hm Hm Merci beaucoup vous avez été très .... Rapide o_O
POur la première je vais revérifier , mais pour la deuxième ça me parait vraiment ... incroyable le résultat lol, pourtant en me relisant j'ai bien écrit l'intégrale ..

J'aimerais aussi , si ovus le voulez bien :) , que vous me fassiez un résumé des hm .. comment dire .. formules d'integrales: comme
(x+1)' (x+1)^3 = [ (x+1)^4/4]'

Car c'est avec ces formules que je m'embrouille le plus , mon livre de Maths m'éclaire peu quand à ce sujet .

Merci encore

par **fonfon** » 12 Avr 2007, 10:57

POur la première je vais revérifier

non, la première est parfaitement correcte

par **Eaglenight** » 12 Avr 2007, 11:00

fonfon a écrit:non, la première est parfaitement correcte

exusez moi je voulais parler de la premiere de fausse que emdro a évoquer

par **emdro** » 12 Avr 2007, 11:04

x^4/(1+x^5) doit te faire penser à du u'/u à un 5 près. Donc une primitive en ln de valeur absolue de u.

Ca marche?

par **fonfon** » 12 Avr 2007, 11:05

exusez moi je voulais parler de la premiere de fausse que emdro a évoquer

emdro a raison il manque du ln

regarde bien

c'est de la forme

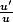
a une constante prés

par **Eaglenight** » 12 Avr 2007, 11:29

AHhhhhhhhhhhhhhhhhhhh ouffff j'ai refait la même erreur que lorsque j'ai demander de l'aide sur cette intégrale il y quelques jours .
Encore une foi exusez moi mais je me suis trompé sur l'intégrale, le (1+x^5) est élevé à la puissance 3 :S:S:S

Encore désolé .

par **emdro** » 12 Avr 2007, 11:38

Ok, dans ce cas 3/40, c'est bon!

par **Eaglenight** » 12 Avr 2007, 11:47

Merci beaucoup :) me reste à regler la 7eme Intégrale de ma liste ! en fait en revérifiant je trouve 1/7

par **emdro** » 12 Avr 2007, 11:49

Oui, c'est u^6*(2u')...

par **Eaglenight** » 12 Avr 2007, 11:50

J'ai fait u(x)^6* [u'(x)] *1/2, on peut faire ça ?

par **emdro** » 12 Avr 2007, 11:52

Non, c'est l'inverse: tu n'as pas u' mais le double: 2u'.
1/2*u', ce serait 1/4+1/(4rac(x)).

par **Eaglenight** » 13 Avr 2007, 08:40

emdro a écrit:

Intégrale de x= 1 à x=4 de ((x/2)+RAC(x)-1)^6(1+(1/RAC(x))) dx = 5/24
si j'ai bien lu, cela donne 279935/448.

Merci j'ai enfin réussi à trouver ce résultat ! en fait je bloquais sur les primitives et dérivés de ce qui touche RAC(x)

Merci à tout ceux qui m'on aider

par **Eaglenight** » 15 Avr 2007, 10:54

Merci jai reussi a trouver ce resultat :)

Sinon pour une autre l'integrale vous pouvez me la verrifier svp ? je ne suis pas sur :) c'est l'integrale de x=PI/2 a x=0 de e^2x [cos²(x)+sin²(x)] = 4e^PI - 4 ?

Vérification d'integrale

Vérification d'integrale

Qui est en ligne