En regardant un peu plus, je pense avoir trouvé une façon de se dispenser des calculs du post. précédent (bonbons/réglisses) et d'un peu mieux visualiser pourquoi on peut raisonner "localement" pour reprendre ton expression.
Par contre, bien que nettement moins calculatoire, je ne suis pas sûr que se soit pour autant accessible pour un Lycéen.
Pour que ce soit plus clair, l'idéal est de modifier légèrement l'énoncé en considérant qu'on a un petit placard à rangement contenant
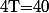
tiroirs dont
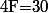
contiennent un fruit (plus court à écrire que "bonbon au fruit") et les
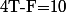
autres un réglisse (idem...).
Chaque enfant ouvre un tiroir au hasard (avec équiprobabilité) et mange son contenu, puis Noémie remet un réglisse dans le tiroir et le referme.
Pour déterminer la proba
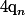
de prendre un fruit lors du

-ième tirage, on utilise la formule des proba totales (encore... :bad: ) en disant que
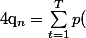
ouvrir le tiroir
\times p()
prendre un fruit sachant que le tiroir

a été ouvert
)
La première proba vaut

(équiprobabilité) et il n'y a rien de "magique" là dessus, mais la deuxième est bêtement (et clairement) égale à la proba que le tiroir
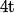
contienne un fruit juste avant le

-ième tirage et ça, c'est "magique", parce que ça veut dire qu'il suffit de s'intéresser
localement à se qui se passe dans un tiroir et pas à ce qui se passe
globalement sur l'ensemble des tiroirs : par exemple, le fait qu'un tiroir contienne ou pas un réglisse
n'est pas indépendant du fait qu'un autre tiroir contienne ou pas un réglisse sauf que... on s'en fout.
Pour terminer le calcul, il faut considérer les deux types de tiroirs :
- Ceux contenant un réglisse dés le départ contiendront à coup sûr un réglisse avant le

-ième tirage donc la proba d'y trouver un fruit est nulle.
- Ceux contenant un fruit au départ (il y en a
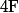
) ont une proba de
^{n-1})
de ne jamais avoir été ouvert au préalable et donc de toujours contenir leur fruit de départ.
Bilan :
^{n-1})
