t.itou29 a écrit:Salut !
Pour l'analyse, je trouve que les problèmes du hmmt sont très intéressants, c'est des problèmes type "olympiades" mais avec de l'analyse.
http://hmmt.mit.edu/archive/problems/ (c'est la partie "calculus" jusqu'en 2011 je crois)
Et sinon un autre problème:
Soit f,g deux fonctions non constantes, dérivables sur R telles que pour tout couple de réels (x;y):
 f(x + y) = f(x)f(y) - g(x)g(y) \\<br />(2) g(x + y) = f(x)g(y) + g(x)f(y) \\<br /> (3) f '(0) = 0)
Montrer que pour tout x:
^2+g(x)^2=1)
Je n'ai pas trop eu le temps d'y réfléchir donc je m'excuse si le raisonnement n'est pas bon.. En particulier je doute de la véracité d'un théorème que j'utilise, que j'ai vu dans mon cours, à savoir:
Théorème fondamental de l'exponentielle:
La fonction exponentielle est l'unique fonction dérivable sur

telle que pour tous réels x et y, on a:
=\exp(x)\times \exp(y))
et
=1)
Corrolaire:
f est une fonction dérivable sur

est telle que:
=f(x) \times f(y) et f(0)=1)
Si et seulement si on a
=e^{xf'(0)}) Démonstration:
Démonstration:Introduisons la fonction g définie par:
=[f(x)]^{\frac{1}{f'(0)}})
On a bien pour tout réel x et y:
=[f(x+y)]^{\frac{1}{f'(0)}}=[f(x) \times f(y)]^{\frac{1}{f'(0)}}=[f(x)]^{\frac{1}{f'(0)}} \times [f(y)]^{\frac{1}{f'(0)}}=g(x) \times g(y))
Par ailleurs, on a aussi pour tout x:
=\frac{1}{f'(0)}f'(x)[f(x)]^{\frac{1}{f'(0)}-1})
D'où:
=\frac{f'(0)}{f'(0)}\times 1^{\frac{1}{f'(0)}-1}=1)
Par le théorème fondamental de l'exponentielle, on a pour tout x:
=e^x \Leftrightarrow f(x)=e^{xf'(0)})
Réciproquement,
=e^{xf'(0)})
, alors on a bien:
=e^{(x+y)f'(0)}=e^{xf'(0)}\times e^{yf'(0)}=f(x)\times f(y))
et
=e^{0f'(0)}=e^0=1)
On admet que ce dernier théorème est toujours vrai lorsque f est à valeurs complexes (ce qui est vraisemblable puisque la fonction exponentielle à les mêmes propriétés dans l'ensemble des nombres complexes).
On reprend maintenant les fonctions f et g non constantes et dérivables sur

définies par:
=f(x)f(y)-g(x)g(y))
=f(x)g(y)+f(y)g(x))
=0)
Déterminons les valeurs de f(0) et g(0).
En prenant x=y=0, on obtient:
=2f(0)g(0)) (1)
(1)et
=[f(0)]^2-[g(0)]^2)
(2)
L'équation (1) permet d'affirmer que
=0)
ou
=\frac{1}{2})
. En supposant que
=\frac{1}{2})
, on peut réécrire (2) ainsi:
]^2=\frac{3}{4})
Ce qui est absurde puisqu'un carré est toujours positif, donc l'opposé d'un carré est toujours négatif, soit différent de
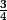
. On a donc
=0)
.
L'équation (2) se réécrit alors:
(1-f(0))=0)
Donc
=0)
ou
=1)
On choisit y=0, on a alors:
=f(x)f(0)-g(x)g(0) \Leftrightarrow f(x)=f(x)f(0))
.
Si on suppose que f(0)=0, alors on pour tout x, on a
=0)
, ce qui est absurde puisque f n'est pas une fonction constante. Donc
=1)
.
On introduit la fonction h, définie pour tout réel x par:
=f(x)+ig(x))
On a alors pour tout réels x et y:
\times h(y)=[f(x)+ig(x)][f(y)+ig(y)]=f(x)f(y)-g(x)g(y)+i[f(x)g(y)+f(y)g(x)]=f(x+y)+ig(x+y)=h(x+y))
On a bien
=h(x)\times h(y))
.
Donc, par le corollaire du théorème fondamental de l'exponentielle, on peut dire que l'on a:
=e^{xh'(0)}=e^{ixg'(0)}=cos(x g'(0))+sin(x g'(0))
Or, puisqu'on a aussi
=f(x)+ig(x))
, on a pour tout x,
[CENTER]
=cos(x g'(0)))
et
=sin(x g'(0)))
[/CENTER]
On pose
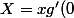)
, on a bien pour tout réel x:
]^2+[g(x)]^2=cos(X)^2+sin(X)^2 \Leftrightarrow [f(x)]^2+[g(x)]^2=1)
En tout cas, merci pour ce problème qui m'a beaucoup plu..! :ptdr:
Bonne soirée !

