Salut, J'ai un éxo sur les limites voici le sujet :
1. Soit F la fonction définie sur R par f(x)= (x +cos(x))/2+sin(x)
Determienr les limites de f en -(inf) et en +(inf)
2. Déterminer la limite en -(inf) de la fonction g définie sur par
g(x)= racine(x2+2) +x
3. Déterminer la limite en +(inf) de la fonction h définie sur par
h(x)= racine(x2+2) -x
Alors pour la 1 j'ai pas réussi, car il me semble que il n'existe pas de limite lorsque x tend vers un infinie pour les fonctions trigonométrique non ?
J'ai essayer longtemps mais je me suis vite décourager... :triste: :triste:
Aidez moi...
Merci
DM sur Limites de fonctions
12 messages
- Page 1 sur 1
Bonjour,
merci de votre réponse,
J'ai essayé de décomposer la fonction f pour avoir x + cos x et 2 + sin x afin de pouvoir encadrer chacune des 2 expressions.
Donc: -1< cos(x) <1
d'où -1+x< cos(x)+ x <1+x
et -1< sin(x) <1
1< sin(x)+2 <3
A ce stade, je ne voit pas trop comment faire car la limite de n'est plus la même de chaque côté... comment faire :hein: :hein: :hein: :hein: :hein:
:triste: :triste:
merci de votre réponse,
J'ai essayé de décomposer la fonction f pour avoir x + cos x et 2 + sin x afin de pouvoir encadrer chacune des 2 expressions.
Donc: -1< cos(x) <1
d'où -1+x< cos(x)+ x <1+x
et -1< sin(x) <1
1< sin(x)+2 <3
A ce stade, je ne voit pas trop comment faire car la limite de n'est plus la même de chaque côté... comment faire :hein: :hein: :hein: :hein: :hein:
:triste: :triste:
A oui désolé, j'ai oublier les parenthèses... !
J'ai encadré (cos(x)+x)/(sin(x)+2)
ce qui donne :
(-1+x)/(sin(x)+2) < (cos(x)+x)/(sin(x)+2) < (1+x)/(sin(x)+2)
or je sais que 1< (sin(x)+2) < 3.
Et je voulais savoir il était possible d'écrire:
(-1+x)/(1) < (cos(x)+x)/(sin(x)+2) < (1+x)/(3)
d'où: (-1+x) < (cos(x)+x)/(sin(x)+2) < (-1+x)/3
Et avec cette expression, puis-je déterminer limite de -1+x pour la lim en +infinie
et pour la lim en -infinie je détermine lim de (-1+x)/3
Est-ce que cela marche ?
Sinon pour votre réponse, pourquoi 1/(sin(x)+2) ?
J'ai encadré (cos(x)+x)/(sin(x)+2)
ce qui donne :
(-1+x)/(sin(x)+2) < (cos(x)+x)/(sin(x)+2) < (1+x)/(sin(x)+2)
or je sais que 1< (sin(x)+2) < 3.
Et je voulais savoir il était possible d'écrire:
(-1+x)/(1) < (cos(x)+x)/(sin(x)+2) < (1+x)/(3)
d'où: (-1+x) < (cos(x)+x)/(sin(x)+2) < (-1+x)/3
Et avec cette expression, puis-je déterminer limite de -1+x pour la lim en +infinie
et pour la lim en -infinie je détermine lim de (-1+x)/3
Est-ce que cela marche ?
Sinon pour votre réponse, pourquoi 1/(sin(x)+2) ?
Oui tu as le droit d'écrire (-1+x)/(1) < (cos(x)+x)/(sin(x)+2) < (1+x)/(3) car sin(x)+2 est de signe constant. (sauf que tu as fait une erreur)
c'est pour cela que je voulais que tu fasses l'encadrement de +2 }) pour être sûre que tu ne fasses pas d'erreur dans les encadrements (d'ailleurs tu t'es trompé).
pour être sûre que tu ne fasses pas d'erreur dans les encadrements (d'ailleurs tu t'es trompé).
et donc après oui tu prends la limite en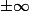
c'est pour cela que je voulais que tu fasses l'encadrement de
et donc après oui tu prends la limite en
Merci j'ai trouvé pour la question 2 par contre pour la question 3 lorsque je fais la partie conjuguée de h(x) je trouve x/(rac(x²+x)+x) .
Donc lorsque je calcule la limite cela me donne de nouveaux une forme indéterminée car lim (rac(x²+x)+x) = + infini .
Or je connais le résultat de ma calculatrice qui affiche 1/2 :help: :help:
Comment faire ??
Donc lorsque je calcule la limite cela me donne de nouveaux une forme indéterminée car lim (rac(x²+x)+x) = + infini .
Or je connais le résultat de ma calculatrice qui affiche 1/2 :help: :help:
Comment faire ??
12 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 93 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
