Devoirs sur les fonctions et limites ou je comprend rien...

[Wi_Zi]

Exercice 3:
On considere la suite (W n) n supérieur ou égal a 1, définie par:
W n= ((5n-1)/(3n))^2
1) la suite (W n) est-elle géométrique?
2)démontrer que, pour tout entier n supérieur ou égal a 1, on a :
(5n+4)/(3n+3) > (5n-1)/(3n) > 1
3)Soient x et y deux réels tels que x>y>1 et n un entier supérieur ou égal a 1. démontrer que x^n+1>y^n (on comparera x^n+1 et y^n à x^n)
4) déduire des deux questions précédentes que la suite (W n) est croissante.
5) Démontrer que, pour tout entier n supérieur ou égal a 1, on a : W n=(4/3)^n
En déduire que la suite (W n) diverge.

Exercice 4 (et le dernier ):
On considere la fonction F définie sur ]-1;+ infini[ par: f(x)=(5x-3)/(x+1)
1)a) étudier les variations de F sur son ensemble de définition.
b) Soit (C) la courbe représentatrice de f dans un repere orthonormal.
i. Montrer que (C) a deux asymptotes
ii. Montrer que la courbe (C) et la droite (Delta) d'équation y=x ont deux points d'intersection.
iii.Dessiner la courbe (C) et la droite (delta).
2) Soit (U n) la suite définie par son premier terme U0=2 et par la relation de récurrence: U n+1= f(U n)= ((5U n)-3)/((U n)+1)
a) faire apparaitre les termes U0, U1, U2 et U3 sur le graphique précédent.
b) Pour tout n appartien au naturel, on pose V n= ((U n)-3)/((U n)-1). Démontrer que la suite (V n) est une suite géométrique puis exprimer V n en fonction de n.
c) En déduire l'expression de U n en fonction de n et calculer la limite de la suite (U n).

De ces deux derniers exos, il me manque le 3, 4 et 5 de l'exercice 3 et le 1)b)iii de l'exercice 4, si quelqu'un peut m'aider...

[fonfon]

re,

3)Soient x et y deux réels tels que x>y>1 et n un entier supérieur ou égal a 1. démontrer que x^n+1>y^n (on comparera x^n+1 et y^n à x^n)

comme n entier >1
on te dit de comparer à et à

on te dit que x>y>1 donc comme x>y (x>1,y>1) on a

de même pour comparer 2 nombres tu peux regarder le signe de leurs differences donc

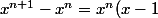or x>1 donc x-1>0 et (car n entier >1)
donc donc

or donc


essaie de continuer l'exo

1)b)iii de l'exercice 4, si quelqu'un peut m'aider...

qu'est-ce qui te gene il suffit de tracer la courbe representative de la fonction f et la droite y=x

[fonfon]

re, pour la question 5) de l'exercice 3 il doit y avoir une erreur d'ennoncé , rien que pour W1 c'est pas bon donc revoir l'ennoncé

[Wi_Zi]

Démontrer que, pour tout entier n supérieur ou égal a 1, on a : W n Supérieur ou égale (4/3)^n
En déduire que la suite (W n) diverge.

Voila l'énoncé est corrigé merci d'avance

[Wi_Zi]

Je n'arrive pas a tracé la courbe et le droite (Exo4 a) iii) ni a placé les points de la question suivante... Si quelqu'un pourrait m'aider...

[anima]

Je n'arrive pas a tracé la courbe et le droite (Exo4 a) iii) ni a placé les points de la question suivante... Si quelqu'un pourrait m'aider...

On considere la fonction F définie sur ]-1;+ infini[ par: f(x)=(5x-3)/(x+1)
1)a) étudier les variations de F sur son ensemble de définition.

Je ne vois pas pourquoi ta fonction est définie uniquement sur ]-1;+inf, mais bon...

(1ere: variation
2nde: quotient des termes déterminants)

f(x) = 0 ssi 5x-3=0; 5x=3; x=3/5
f'(x) =
Je continuerai plus tard

[Wi_Zi]

Courbe tracée, je ne comprend pas où mettre les points U0 U1 U2 et U3...

[fonfon]

Démontrer que, pour tout entier n supérieur ou égal a 1, on a : W n Supérieur ou égale (4/3)^n

ça marche toujours pas

par ex pour n=4



et



donc

donc revoit Wn du depart je pense que c'est puissance n et non au carré