Devoirs sur les fonctions et limites ou je comprend rien...

par **Wi_Zi** » 17 Juil 2007, 20:15

Bonjour a tous, voila, j'ai un devoir a faire, mais je ne comprend pas du tout... J'aimerais une explication sur des exercices que je donne ci-dessous. Merci

Exercice 1:
Trois nombres réels a, b et c sont, dans cet ordre, trois termes consécutifs d'une suite arithmétique croissante. Leur somme est 27/2 et la somme de leurs inverses est 109/126.
Déterminer les trois nombres a, b et c.

Exercice 2:
On considere la suite (U n)n appartient au naturel, définie par:
U 0=27 ; U 1=27.27; ... ; U n= 27.27272727...27
Le terme de rang n contenant 2n décimales alternativements égales a 2 et 7
1) on définit la suite (V n)n supérieur ou égal a 1, par: V n=U n-U n-1
Calculer V1, V2 et V3
2)Montrer que la suuite (V n) est une suite géométrique.
3) Calculer la somme S n des n premiers termes de la suite (V n) et calculer la limite S n quand n tend vers + infini.
4)En déduire que la suite (U n) converge vers 300/11

Exercice 3:
On considere la suite (W n) n supérieur ou égal a 1, définie par:
W n= ((5n-1)/(3n))²
1) la suite (W n) est-elle géométrique?
2)démontrer que, pour tout entier n supérieur ou égal a 1, on a :
(5n+4)/(3n+3) > (5n-1)/(3n) > 1
3)Soient x et y deux réels tels que x>y>1 et n un entier supérieur ou égal a 1. démontrer que x^n+1>y^n (on comparera x^n+1 et y^n à x^n)
4) déduire des deux questions précédentes que la suite (W n) est croissante.
5) Démontrer que, pour tout entier n supérieur ou égal a 1, on a : W n=(4/3)^n
En déduire que la suite (W n) diverge.

Exercice 4 (et le dernier :++: ):
On considere la fonction F définie sur ]-1;+ infini[ par: f(x)=(5x-3)/(x+1)
1)a) étudier les variations de F sur son ensemble de définition.
b) Soit (C) la courbe représentatrice de f dans un repere orthonormal.
i. Montrer que (C) a deux asymptotes
ii. Montrer que la courbe (C) et la droite (Delta) d'équation y=x ont deux points d'intersection.
iii.Dessiner la courbe (C) et la droite (delta).
2) Soit (U n) la suite définie par son premier terme U0=2 et par la relation de récurrence: U n+1= f(U n)= ((5U n)-3)/((U n)+1)
a) faire apparaitre les termes U0, U1, U2 et U3 sur le graphique précédent.
b) Pour tout n appartien au naturel, on pose V n= ((U n)-3)/((U n)-1). Démontrer que la suite (V n) est une suite géométrique puis exprimer V n en fonction de n.
c) En déduire l'expression de U n en fonction de n et calculer la limite de la suite (U n).

Voila merci d'avance pour ceux qui vont m'aider car j'ai vraiment besoin d'aide...

par **coco76890** » 17 Juil 2007, 20:22

exercice 1

on te dis que a+b+c= 27/2
et que 1/a+1/b+1/c= 109/126

tu resouds une équation a 3 inconus avec deux equations commence par resoudre ton système en faisant comme si un des termes n'existé pas tu vas avoir un système bisar avec 2inconu puisque tu auras exprimé par exemple a en fondtion de b et c

ensuite tu formes des égalités et hop magique tu retrouves un système a 2 inconus !

enfin il me semble que c'est la méthode que j'ai retenue, a confirmé

par **coco76890** » 17 Juil 2007, 20:27

pour l'exercice 2 il est pas bien compliquer il suffit d'appliquer tes formules du cours et pour la question 1 d'utiliser U(0) et U(1) et tu trouveras V1 V2 et V3

et l'exercice 4 regarde ton cours si tu étais en terminale cette année t'as du faire des exercices du meme style car moi j'en ai fait des très très similaires!! pour la question 1 par exemple il suffit de calculer la dérivée et de faire le tableau de signe et t'en déduit ton tableau de variation

pour qla questoin b de calculer les limites de la fonction sur son domaine de définitions et de calculer pour ii la limite de f(x)-y quand x->+oo

enfin un exercice banale réfléchit !!

par **coco76890** » 17 Juil 2007, 20:27

je t'accorde que l'exo 3 est un peu plus complexe

par **Wi_Zi** » 17 Juil 2007, 20:28

B je passe en terminale, mais cet année fut dure pour moi, et si vous pouvez un peu détailler sa m'aiderais vachement... Merci

par **Wi_Zi** » 17 Juil 2007, 20:32

Merci pour l'exercice 1 je vien de le finir... :)

par **fonfon** » 18 Juil 2007, 07:16

salut,

Exercice 4 (et le dernier ):
On considere la fonction F définie sur ]-1;+ infini[ par: f(x)=(5x-3)/(x+1)
1)a) étudier les variations de F sur son ensemble de définition.
b) Soit (C) la courbe représentatrice de f dans un repere orthonormal.
i. Montrer que (C) a deux asymptotes
ii. Montrer que la courbe (C) et la droite (Delta) d'équation y=x ont deux points d'intersection.
iii.Dessiner la courbe (C) et la droite (delta).
2) Soit (U n) la suite définie par son premier terme U0=2 et par la relation de récurrence: U n+1= f(U n)= ((5U n)-3)/((U n)+1)
a) faire apparaitre les termes U0, U1, U2 et U3 sur le graphique précédent.
b) Pour tout n appartien au naturel, on pose V n= ((U n)-3)/((U n)-1). Démontrer que la suite (V n) est une suite géométrique puis exprimer V n en fonction de n.
c) En déduire l'expression de U n en fonction de n et calculer la limite de la suite (U n).

1)a) variation calcule la dérivée c'est de la forme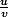

de dérivée

,tu devrais trouver

donc f'(x) est ... donc f est ...

b)i) il faut calculer les limites aux bornes de l'ensemble de definition tu devrais trouver 2 asymptotes qui ont pour equation y=5 et x=-1

ii) tu peux resoudre f(x)=x et montrer que l'on a bien 2 points d'intersections

iii) à faire

2) a) regarde ds ton cours de 1ere tu vas te sevir de la courbe C et de l'equation y=x

b) calcule

et montre que on a qq chose de la forme

avec q la raison et ensuite c'est du cours

c) je te laisse reflechir

si j'ai le temps je repasserai pour les 2 autres mais avec le cours ils sont largement abordables

par **Wi_Zi** » 18 Juil 2007, 11:50

Merci beaucoup pour vos réponses elles m'aident grandement :)

par **coco76890** » 19 Juil 2007, 10:14

excuse moi d'avoir était si franc alors !! dsl

mais les exos resemble a ceux de terminale c'est pour ca ! excuse moi bon alors attend je vais relire tes énoncés

pour l'exercice 1 je pense t'avoir donné suffisament d'explication cependant si cela ne te convient pas dit le moi je tenterais d'etre plus précis !

pour l'exercice 2 il suffit comme je l'ai dit de regarder les formules du cours tout y ai écrit je te les redonnes

pour montrer qu'une suite est géomètrique on effectue le calcul : Un+1 / Un

pour calculer la somme d'une suite géométrique on fait : premier terme * [( 1 - la raison a la puissance nombre de terme)/ (1 - la raison)]

la raison tu l'obtiens grâce a la question précédente car lorsque tu auras montrer que la suite est géométrique tu devrais trouver un nombre appartenant a R qui ne doit pas etre en fonction de Un ou de n par exemple 1/9 alors ici toujours dans mon exemple 1/9 est la raison

ensuite bah tu calcules la limite si tu n'y parvient as dit le moi je tenterais de la resoudre et de t'aider

par **Wi_Zi** » 19 Juil 2007, 11:58

Pour l'exercice 1, je croyais y etre arrivé mais non, je trouve b=9/2 mais apres je trouve des nombres improbables, quelqu'un pourrais m'expliquer?

par **fonfon** » 19 Juil 2007, 12:56

salut,

conne a,b,c sont les termes consecutifs d'une suite arithmetique croissante tu peux ecrire que a=b-r et c=b+r avec r la raison et ensuite tu traduis ton ennoncé je n'ai pas fais les calculs

par **oscar** » 19 Juil 2007, 22:02

Bonsoir

Soit les nombres x-r; x; x désignant les nombres a ; b; c )

x-r + x + x+r = 27/2

=> x= 9 / 2 soit b

1/(x-r) + 1 / x + 1 / (x+r) = 109/126

Il faut remplacer x par 9/2 pour trouver r puis déterminer a et c

par **fonfon** » 20 Juil 2007, 06:32

oscar a écrit:Soit les nombres x-r; x; x désignant les nombres a ; b; c )

atenntion c'est x-r ; x ; x+r tu l'as bien ecris apres oscar mais notre ami(e) risque de ne pas s'y retrouver

par **oscar** » 20 Juil 2007, 11:08

Bojour

Je continue1/(x-r) + 1/x+ 1/(x-r) = 109/126
remplaçons 1/x par 2/9
Il vient 1/(x-r) + 2/9 + 1/ (x+r) = 109/126

1/(x-r) + 1/(x+r) = 109/126 - 2/9 =729/9*126= 9/14

(x+r)/x²-r²) + (x-r)/(x²-r²) = 9/14
=> 2x/(x²-r²) = 9/14
=> 9/ (81/4- r²) = 9/14

=> 81/4 - r² = 14
=> r² := 25/4
r= + ou - 5/2 gardons 5/2( on aurait les mêmes solutions..)

a= 4/2 ; b = 9/2 et c=14/2 soit a=2; b = 4,5 et c= 7

par **Wi_Zi** » 20 Juil 2007, 13:41

Bonjour, merci pour votre aide, mais je ne comprend toujours pas ni l'exo 3 ni le 4... Si quelqu'un pouvait m'aider... Merci d'avance

par **oscar** » 20 Juil 2007, 13:45

Voici la PREUVE

J' ai trouvé les nombres a= 2; b= 9/2 et c = 7

a + b+ c = 2 + 9/2+ 7 = 9 + 9/2 = 27/2

/a + 1/b + 1/c = 1/2 + 2/9 + 1/7 =

.....................= ( 63 + 28 + 18) / 126 = 109/126

par **fonfon** » 20 Juil 2007, 13:51

re,

pour le 4) je t'ai donné plein de pistes as-tu au moins essayer de chercher ?

par **Wi_Zi** » 20 Juil 2007, 14:09

Dans ton avant derniere réponses, c=7 pas 14 et ensuite oui j'ai cherché mais je ne comprend vraiment rien... Désolé je ne suis pas surdoué, je trouve des réponses impossibles...

par **Wi_Zi** » 20 Juil 2007, 14:49

J'ai trouvé le 1) de l'exo 3 mais le reste je planche trop... Aidez moi...

par **Wi_Zi** » 20 Juil 2007, 15:00

2) de l'exo 3 trouver

Devoirs sur les fonctions et limites ou je comprend rien...

Devoirs sur les fonctions et limites ou je comprend rien...

Qui est en ligne