Bonjour,
Suite au sujet de bac 1986, je vous propose d'essayer de faire le maximum d'épreuves de maths de bac de la série qu'on appellait C à l'époque ( < 1990 ). Mais en fait, il s'agit de le faire en utilisant seulement les connaissances du programme de terminale de 2015, et de voir quelle proportion est faisable par un élève d'aujourd'hui. On pourra admettre certaines définitions comme il est d'usage de le faire ( par exemple, on admettra que le barycentre de trois points est défini par... ). Je me porte comme cobaye, puisque je viens de passer mon bac s, et que je suis tout à fait représentatif des élèves de Ts.
Je mettrai un lien à chaque fois.
Pour le bac 1987, voici le lien: http://www.apmep.fr/IMG/pdf/ParisCjuin1987.pdf
Pour ce bac-ci, on a:
- exercice 1: complexes et barycentres
- exercice 2: géométrie euclidienne
- problème: étude d'une fonction trigonométrique et approximation de son intégrale
Vous pouvez participer ou me corriger si j'écris n'importe quoi. :lol3:
( Pour info après m'y être attardé un peu, il est bien plus dur que celui de 1986... qui lui même n'était pas si simple... )
Sujet bac 1987
7 messages
- Page 1 sur 1
Salut !
J'essaierais de voir ça :++:
Le barycentre n'est plus au programme de 1S, il me semble.
De même les similitudes, ne sont plus au programme de TS spé.
J'essaierais de voir ça :++:
Le barycentre n'est plus au programme de 1S, il me semble.
De même les similitudes, ne sont plus au programme de TS spé.
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Voici une première ébauche de ce que je proposerai pour l'exercice 1 :
Avant tout, O étant considéré comme l'origine du repère donné, O est l'isobarycentre des points A, B, C et D équivaut à dire que a + b + c + d=0.
1. En effectuant la moyenne arithmétique des affixes des points I et J, on en conclut que O est le milieu de [IJ].
2. A (resp. B, C et D) peut se voir comme l'image de B (resp. C, D et A) par la rotation de centre M (resp. N, Q et P) ; traduire alors ces égalités en termes de nombres complexes.
3. Utiliser la question précédente en sommant membre à membre les quatre égalités.
5. Je ne vois pas pour l'instant...
6. Si I=J alors ABCD est un parallélogramme.
On a K=L=O et MNPQ forme un carré de centre O.
Après j'ai pas eu le temps de trop regardé.
Je ne dévoile pas tout histoire de laisser les autres y réfléchir éventuellement :+++: @+
Avant tout, O étant considéré comme l'origine du repère donné, O est l'isobarycentre des points A, B, C et D équivaut à dire que a + b + c + d=0.
1. En effectuant la moyenne arithmétique des affixes des points I et J, on en conclut que O est le milieu de [IJ].
2. A (resp. B, C et D) peut se voir comme l'image de B (resp. C, D et A) par la rotation de centre M (resp. N, Q et P) ; traduire alors ces égalités en termes de nombres complexes.
3. Utiliser la question précédente en sommant membre à membre les quatre égalités.
5. Je ne vois pas pour l'instant...
6. Si I=J alors ABCD est un parallélogramme.
On a K=L=O et MNPQ forme un carré de centre O.
Après j'ai pas eu le temps de trop regardé.
Je ne dévoile pas tout histoire de laisser les autres y réfléchir éventuellement :+++: @+
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Salut,
et merci pour ta contribution. Honnêtement je n'aurais pas été capable de faire ce que tu as fait en géométrie. Je pense que tout le monde s'accordera à dire qu'aucun terminale s standard ne saurait résoudre cet exercice avec des barycentres et des transformations du plan, savamment mêlés aux complexes. J'ai lu une fois tes réponses, mais demain j'aurai oublié alors je chercherai de nouveau et je comparerai... Je commence à comprendre que la différence de niveau se situe sûrement au niveau de la géométrie, où les exercices me semblent plus recherchés et de recherche.
Mais sinon j'ai passé un peu de temps sur le problème d'analyse, qui est certes plus long mais beaucoup plus simple. Finalement j'ai fini la première partie sans utiliser de théorèmes ni de techniques hors programme. Je mettrai ce que j'ai trouvé demain, et en même temps finirai la deuxième partie...
et merci pour ta contribution. Honnêtement je n'aurais pas été capable de faire ce que tu as fait en géométrie. Je pense que tout le monde s'accordera à dire qu'aucun terminale s standard ne saurait résoudre cet exercice avec des barycentres et des transformations du plan, savamment mêlés aux complexes. J'ai lu une fois tes réponses, mais demain j'aurai oublié alors je chercherai de nouveau et je comparerai... Je commence à comprendre que la différence de niveau se situe sûrement au niveau de la géométrie, où les exercices me semblent plus recherchés et de recherche.
Mais sinon j'ai passé un peu de temps sur le problème d'analyse, qui est certes plus long mais beaucoup plus simple. Finalement j'ai fini la première partie sans utiliser de théorèmes ni de techniques hors programme. Je mettrai ce que j'ai trouvé demain, et en même temps finirai la deuxième partie...
La modestie s'apprend par la répétition de l'échec.
La question 5 de l'exercice 1 (la plus dure) est faisable par un élève de TS avec le programme d'aujourd'hui à condition qu'il sache traduire la rotation d'angle droit direct avec les complexes (oui, il sait).
Pour montrer r(J)=K par le quart de tour direct de centre O, il suffit de montrer que : o(1-i) = k-i*j, avec o affixe de O, j affixe de J.
On l'obtient par j=(a+c)/2, b+d=4o-(a+c), k=(m+p)/2, m et p obtenus dans la question 2), en additionnant m+p. On obtient k-i*j = j - i*(2o-j). En divisant le tout par 1-i, on obtient l'expression cherchée.
Je vais voir la suite si j'ai le temps.
Pour montrer r(J)=K par le quart de tour direct de centre O, il suffit de montrer que : o(1-i) = k-i*j, avec o affixe de O, j affixe de J.
On l'obtient par j=(a+c)/2, b+d=4o-(a+c), k=(m+p)/2, m et p obtenus dans la question 2), en additionnant m+p. On obtient k-i*j = j - i*(2o-j). En divisant le tout par 1-i, on obtient l'expression cherchée.
Je vais voir la suite si j'ai le temps.
Re,
Finalement j'ai pas eu beaucoup de temps jusqu'à maintenant pour travailler, mais je viens de m'y pencher ce soir et j'ai fini la partie 1) de l'exercice sur les fonctions ( avec du mal ). Il ne me reste qu'à recopier ( je mettrai ce que j'ai trouvé petit à petit ).
Problème:
Partie 1)
1) Pour x>0, sin(x) et x dérivables sur R*+, et = \frac {sin(x)}{x}) définie sur R*+ ( car x différent de 0 ). On en déduit f dérivable sur R*+, de dérivée f' tel que pour tout x>0,
définie sur R*+ ( car x différent de 0 ). On en déduit f dérivable sur R*+, de dérivée f' tel que pour tout x>0,  = \frac {xcos(x) - sin(x)}{x^2})
2a) On distingue les cas x=0 et x>0
- x=0 alors=1 \ne 0)
- x>0 alors=0 \Longleftrightarrow sin(x)=0 \Longleftrightarrow x=n\Pi ( n \in \mathbb{N} ))
On peut donc classer ces nombres en une suite a(n) tel que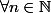 ,
,  = n\Pi)
2b) x>0 alors 1/x > 0. Alors f est de même signe que sin(x). On peut utiliser la suite a(n) précédemment définie pour étudier le signe de sin(x):
- Si;a(n+1)]) et n pair ( n=2k ), alors
et n pair ( n=2k ), alors 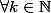 ,
, ;a(2k+1)] = [ 2k\Pi ; 2k\Pi + \Pi ]) . Mais sin(x) étant 2pi-périodique, sin est donc de même signe sur [ 0;pi ], donc positive. Donc sur [a(n);a(n+1)], n pair, sin(x) > 0 d'où f(x) > 0
. Mais sin(x) étant 2pi-périodique, sin est donc de même signe sur [ 0;pi ], donc positive. Donc sur [a(n);a(n+1)], n pair, sin(x) > 0 d'où f(x) > 0
- Si;a(n+1)]) et n impair ( n=2k+1 ), alors
et n impair ( n=2k+1 ), alors 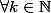 ,
, ;a(2k+2)] = [ 2k\Pi + \Pi ; 2k\Pi + 2\Pi ]) . Mais sin(x) étant 2pi-périodique, sin est donc de même signe sur [ pi;2pi ], donc négative. Donc sur [a(n);a(n+1)], n impair, sin(x) 0
. Mais sin(x) étant 2pi-périodique, sin est donc de même signe sur [ pi;2pi ], donc négative. Donc sur [a(n);a(n+1)], n impair, sin(x) 0
D'où l'inégalité souhaitée \leq \frac{1}{x})
De plus ces deux fonctions x-->-1/x et x-->1/x tendent vers 0 en + l'infini, par le théorème des gendarmes, lim(x-->+inf) f(x) = 0.
3b)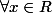 ,
,  = 1/x \Longleftrightarrow sin(x)=1 \Longleftrightarrow x = \Pi/2 + 2k\Pi) ( k étant un entier relatif quelconque ). Or ici x>0 donc
( k étant un entier relatif quelconque ). Or ici x>0 donc  donc k>-1/4 mais comme k appartient à Z, alors
donc k>-1/4 mais comme k appartient à Z, alors 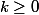 et donc k appartient à N.
et donc k appartient à N.
On peut arranger ces nombres en une suite b(k) tel que pour tout k de N, = \Pi/2 + 2k\Pi) .
.
Ensuite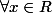 ,
,  = -1/x \Longleftrightarrow sin(x)=-1 \Longleftrightarrow x = \3Pi/2 + 2k\Pi) ( k étant un entier relatif quelconque ). Or ici x>0 donc
( k étant un entier relatif quelconque ). Or ici x>0 donc  donc k>-3/4 mais comme k appartient à Z, alors
donc k>-3/4 mais comme k appartient à Z, alors 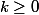 et donc k appartient à N.
et donc k appartient à N.
On peut arranger ces nombres en une suite c(k) tel que pour tout k de N, = 3\Pi/2 + 2k\Pi) .
.
3c) Avec l'inégalité précédente ( \leq \frac{1}{x}) ), on trouve:
), on trouve:
- C est au dessus de H-, les courbes se coupent en b(k), k appartenant à N.
- C est au dessous de H+, les courbes se coupent en c(k), k appartenant à N.
( Pour les tangentes je galère un peu, je complèterai plus tard ).
4a) tan(x) - x dérivable sur [0;2pi], de dérivée^2}}-1) .
.
Sur [0;2pi], \leq 1) donc
donc }^2 \leq 1) ,
, ^2}} \geq 1) et donc
et donc ^2}}-1 \geq 0)
Donc tan(x)-x est croissante sur [0;2pi]
- Comme tan(0)-0=0 alors tan(x)-x est positive sur [0;pi/2[. ( En effet, f n'est pas continue en pi/2 ).
- Sur ]pi/2;3pi/2 [, on peut trouver deux valeurs tel que tan(x) -x soit > ou 0 sur ] x1 ; 3pi/2 [
- Enfin tan(2pi) - 2pi 0 d'où tan(x) - x 0, f' du signe de tan(x) - x.
On en déduit le tableau de signe de f' sur [0;2pi], c'est à dire:
Négatif sur [0;pi/2[
Négatif sur ]pi/2 ; x1[ , positif sur ]x1;3pi/2[
Positif sur ]3pi/2;2pi]
4b) La fonction tan(xk) -xk admet comme dérivée^2}}-1) . On a vu que ce nombre était positif donc tan(xk) - xk est croissante sur tout intervalle
. On a vu que ce nombre était positif donc tan(xk) - xk est croissante sur tout intervalle  .
.
On montre ensuite que cette fonction n'étant pas majorée et croissante, elle admet une limite en +inf, donc au moins une valeur positive dans tout intervalle . De plus
. De plus =0) pour tout k ( pi-périodicité de tan ), donc
pour tout k ( pi-périodicité de tan ), donc -k\Pi=-k\Pikpi puisque [TEX] tan(k\Pi)-k\Pi \lt 0)
4c) Sur l'intervalle ,
,
cos(x)>0 si k est pair --> f' de signe contraire à tan(x)-x ;
cos(x) f' de même signe que tan(x)-x
Ensuite, on peut découper tout intervalle [xk; xk+1] en , sachant que pour tout k, tan(x)-x>0 sur
, sachant que pour tout k, tan(x)-x>0 sur  et tan(x)-x 0 sur
et tan(x)-x 0 sur  ( même signe que tan(x)-x ) et f'>0
( même signe que tan(x)-x ) et f'>0  ( signe contraire à tan(x)-x )
( signe contraire à tan(x)-x )
Donc f' négative sur tout intervalle [ ak ; ak+1 ], k pair , et positive sur tout intervalle [ ak ; ak+1 ], k impair.
5a) Soit = sin(x) - x + \frac {{x}^3}{6})
Alors = cos(x) - 1 + \frac {{x}^2}{2})
Et = -sin(x) + x)
Et enfin = -cos(x) + 1)
Mais -cos (x) + 1 > 0 d'où h'''(x)>0 d'où h''(x) croissante mais h''(0)=0 d'où h''(x)>0 donc h'(x) croissante, mais h'(0)=0, d'où h'(x)>0, donc h croissante mais encore une fois h(x)=0 donc h(x)>0.
Donc h positive d'où -h négative, ce qui s'écrit \leq 0 \Longleftrightarrow x -sin(x) \leq \frac {{x}^3}{6})
Enfin pour x-sin(x), la dérivée donne 1-cos(x) > 0 donc x-sin(x) croissante mais en 0 x-sin(x)=0, donc pour x>0, x-sin(x)>0.
D'où l'inégalité cherchée.
5b) Si f dérivable en 0, alors la limite lim(h-->0) f(a+h)-f(a)/h existe et est finie.
On a-f(a)}{h} = \frac{f(h) - f(0)}{h} = \frac{\frac{sin(h)}{h} - 1}{h} = \frac{sin(h) - h}{h^2})
Mais d'après le 5a) - h}{h^2} \leq 0)
En passant à la limite quand h-->0, comme -h/6 tend vers 0, alors d'après le théorème de gendarmes:
lim(h-->0) f(a+h)-f(a)/h = 0
Donc f dérivable en 0 et f'(0)=0
6)a) Variations sur [0;3pi]
[0;x1] : décroissante
[x1;x2]: croissante
[x2;3pi]: décroissante
Finalement j'ai pas eu beaucoup de temps jusqu'à maintenant pour travailler, mais je viens de m'y pencher ce soir et j'ai fini la partie 1) de l'exercice sur les fonctions ( avec du mal ). Il ne me reste qu'à recopier ( je mettrai ce que j'ai trouvé petit à petit ).
Problème:
Partie 1)
1) Pour x>0, sin(x) et x dérivables sur R*+, et
2a) On distingue les cas x=0 et x>0
- x=0 alors
- x>0 alors
On peut donc classer ces nombres en une suite a(n) tel que
2b) x>0 alors 1/x > 0. Alors f est de même signe que sin(x). On peut utiliser la suite a(n) précédemment définie pour étudier le signe de sin(x):
- Si
- Si
D'où l'inégalité souhaitée
De plus ces deux fonctions x-->-1/x et x-->1/x tendent vers 0 en + l'infini, par le théorème des gendarmes, lim(x-->+inf) f(x) = 0.
3b)
On peut arranger ces nombres en une suite b(k) tel que pour tout k de N,
Ensuite
On peut arranger ces nombres en une suite c(k) tel que pour tout k de N,
3c) Avec l'inégalité précédente (
- C est au dessus de H-, les courbes se coupent en b(k), k appartenant à N.
- C est au dessous de H+, les courbes se coupent en c(k), k appartenant à N.
( Pour les tangentes je galère un peu, je complèterai plus tard ).
4a) tan(x) - x dérivable sur [0;2pi], de dérivée
Sur [0;2pi],
Donc tan(x)-x est croissante sur [0;2pi]
- Comme tan(0)-0=0 alors tan(x)-x est positive sur [0;pi/2[. ( En effet, f n'est pas continue en pi/2 ).
- Sur ]pi/2;3pi/2 [, on peut trouver deux valeurs tel que tan(x) -x soit > ou 0 sur ] x1 ; 3pi/2 [
- Enfin tan(2pi) - 2pi 0 d'où tan(x) - x 0, f' du signe de tan(x) - x.
On en déduit le tableau de signe de f' sur [0;2pi], c'est à dire:
Négatif sur [0;pi/2[
Négatif sur ]pi/2 ; x1[ , positif sur ]x1;3pi/2[
Positif sur ]3pi/2;2pi]
4b) La fonction tan(xk) -xk admet comme dérivée
On montre ensuite que cette fonction n'étant pas majorée et croissante, elle admet une limite en +inf, donc au moins une valeur positive dans tout intervalle
4c) Sur l'intervalle
cos(x)>0 si k est pair --> f' de signe contraire à tan(x)-x ;
cos(x) f' de même signe que tan(x)-x
Ensuite, on peut découper tout intervalle [xk; xk+1] en
Donc f' négative sur tout intervalle [ ak ; ak+1 ], k pair , et positive sur tout intervalle [ ak ; ak+1 ], k impair.
5a) Soit
Alors
Et
Et enfin
Mais -cos (x) + 1 > 0 d'où h'''(x)>0 d'où h''(x) croissante mais h''(0)=0 d'où h''(x)>0 donc h'(x) croissante, mais h'(0)=0, d'où h'(x)>0, donc h croissante mais encore une fois h(x)=0 donc h(x)>0.
Donc h positive d'où -h négative, ce qui s'écrit
Enfin pour x-sin(x), la dérivée donne 1-cos(x) > 0 donc x-sin(x) croissante mais en 0 x-sin(x)=0, donc pour x>0, x-sin(x)>0.
D'où l'inégalité cherchée.
5b) Si f dérivable en 0, alors la limite lim(h-->0) f(a+h)-f(a)/h existe et est finie.
On a
Mais d'après le 5a)
En passant à la limite quand h-->0, comme -h/6 tend vers 0, alors d'après le théorème de gendarmes:
lim(h-->0) f(a+h)-f(a)/h = 0
Donc f dérivable en 0 et f'(0)=0
6)a) Variations sur [0;3pi]
[0;x1] : décroissante
[x1;x2]: croissante
[x2;3pi]: décroissante
La modestie s'apprend par la répétition de l'échec.
7 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 74 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
